Blockschulung
Navigationsschule

Thema
Zusatzblatt Navigation
Hier werden noch weitere Informationen aufgeführt, die über die ‚Basisnavigation‘ der Blockschulung hinausgehen. Einige sind einfach zu verstehen, andere sehr komplex.
Auch wird auf weitere Faktoren eingegangen, die in der Navigation und im Flugbetrieb normalerweise berücksichtigt werden müssen, in 'IL-2: Great Battles Series' aber keine Auswirkungen haben.
Navigatorische Aspekte die für IL2: GB keine Relevanz haben
In der realen Navigation beeinflussen noch weitere Faktoren unseren Kompass, und dadurch auch die Flugplanung…
Diese sind zwar in IL-2: Great Battles Series momentan nicht implementiert, können aber in anderen Simulationen (z.B. Cliffs of Dover) zum Tragen kommen.
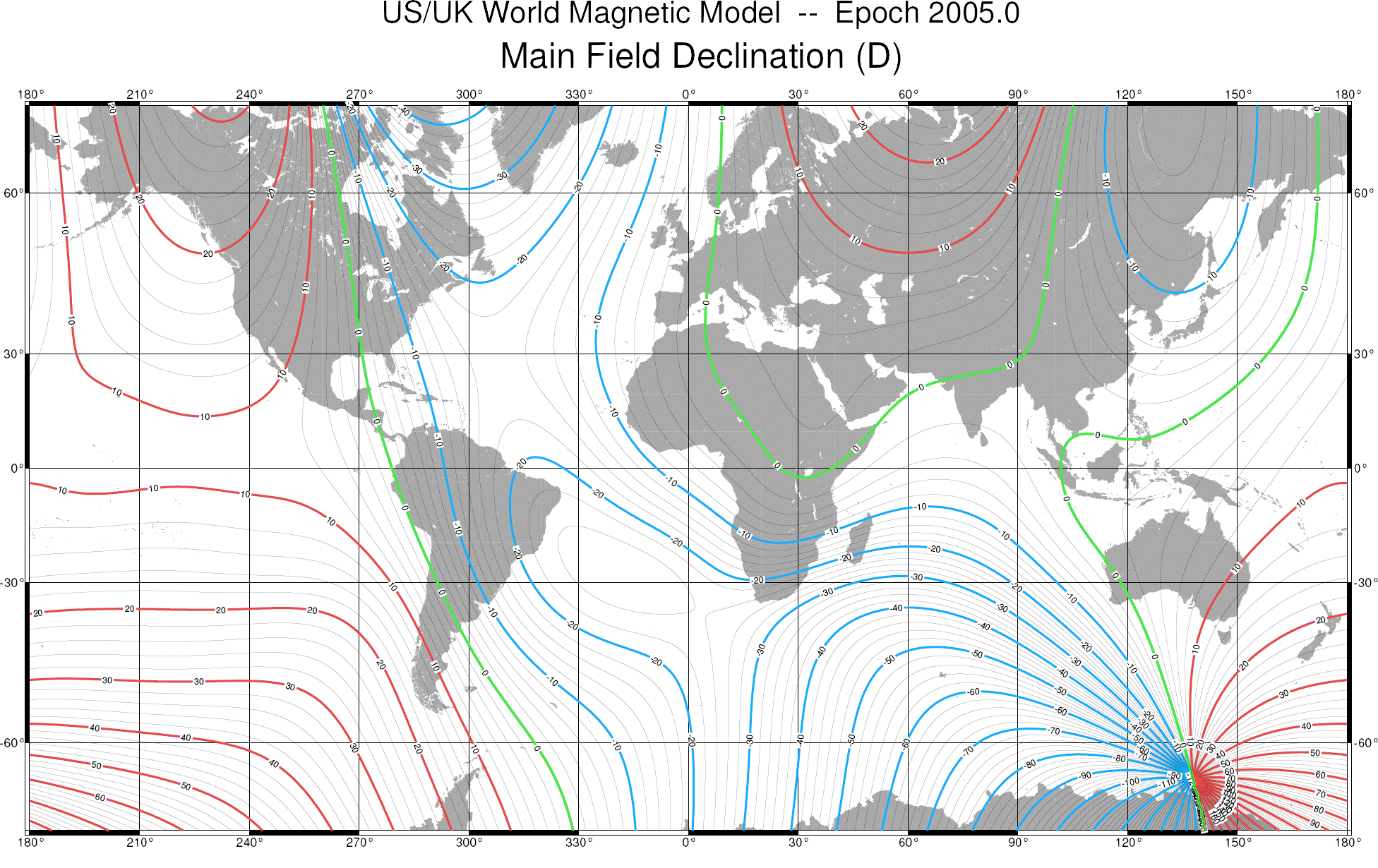
Deklination (Ortsmissweisung)
Da die Verbindungslinie der magnetischen Pole gegenüber der Erdachse um etwa 11,5° geneigt ist, liegen die magnetischen Pole derzeit etwa 2000 km von den geographischen Polen entfernt.
Die magnetischen Pole verändern ihre Lage im Verlauf der Zeit, weil der Erdmagnetismus auf veränderlichen Strömungen im metallischen Erdkern beruht. Zusätzlich wird der Verlauf der magnetischen Feldlinien von den örtlichen geologischen Gegebenheiten (z. B. eisenhaltigem Gestein) beeinflusst.
Diese beiden Faktoren bewirken, dass die Abweichung der Kompassnadel von der geografischen Nordrichtung an jedem Ort der Erde unterschiedlich ist. Diese Abweichung wird Ortsmissweisung oder Deklination genannt.
Es ist nicht sicher, wer diese zuerst erkannte.
Jedoch gilt als gesichert, dass Georg von Peuerbach der erste war, der über die Missweisung schrieb. Der älteste erhaltene Kompass, bei dem die Missweisung eingezeichnet ist, stammt von Peuerbach. Ein Kreiselkompass zeigt keine Deklination, da er unabhängig vom Erdmagnetfeld arbeitet.
Jedoch gilt als gesichert, dass Georg von Peuerbach der erste war, der über die Missweisung schrieb. Der älteste erhaltene Kompass, bei dem die Missweisung eingezeichnet ist, stammt von Peuerbach. Ein Kreiselkompass zeigt keine Deklination, da er unabhängig vom Erdmagnetfeld arbeitet.
Isogonenkarte zur Darstellung der Deklination weltweit von 2005
Deviation
Als Deviation werden Abweichungen bezeichnet, die durch magnetische Felder in der Nähe des Kompasses hervorgerufen werden können. Solche Felder werden durch magnetische oder magnetisierbare Gegenstände und Geräte sowie durch fließenden Wechsel- oder Gleichstrom erzeugt.
Eine mögliche Gegenmaßnahme besteht darin, einen Mutterkompass an einer besser geeigneten Stelle als im Cockpit des Flugzeuges unterzubringen.
Ansonsten oder zusätzlich werden zur Kompensation größerer Abweichungen entweder Magnetnadeln an dafür vorgesehenen Stellen in das Kompassgehäuse eingesetzt (z. B. Ludolph-Kompass) oder beweglich gelagerte Magnete im Kompassgehäuse über Stellschrauben entsprechend justiert (z. B. Airpath-Kompass).
Um diese Kompensierung zu erreichen, wird das Flugzeug langsam um die durch den Kompass führende Hochachse gedreht, die optische Peilung einer in ihrer geografischen Ausrichtung bekannten Linie beobachtet und mit der Kompassanzeige verglichen und die Abweichung notiert.
Verbleibende Rest- und Anzeigefehler, die unter 5° liegen sollen, werden in eine Deviationstabelle eingetragen, von der zu jedem Kompasskurs die dazugehörige Korrektur abgelesen werden kann.
Die Kompensation wird nach Werftaufenthalten wiederholt.
In der allgemeinen Luftfahrt muss die Deviation nach bestimmten Veränderungen am Flugzeug oder in festgelegten Zeitabständen überprüft und der Kompass erneut kompensiert werden. Entsprechende Vorgaben finden sich beispielsweise in den Flug- und Betriebshandbüchern.
Hier erneut die in der kompletten Schulung genutzte Deviationstabelle für die Bf-109
| Kurs nach Karte | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deviation | -2 | -1 | 0 | 2 | 3 | 4 | 4 | 3 | 3 | 2 | 1 | 1 | -1 | -3 | -4 | -3 | -1 | 0 | 0 |
| Kurs nach Karte | 180 | 190 | 200 | 210 | 220 | 230 | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 | 360 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deviation | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 0 | -2 | -3 | -3 | -2 | 0 | 1 | 2 | 1 | -1 | -2 | -2 |
Auswirkung auf die Flugplanung
Sofern Deviation und/oder Ortsmissweisung im Flug zum Tragen kommen, weil diese normalen Abweichungen simuliert werden oder wir in der realen Welt mit echten Gerätschaften hantieren müssen wir diese Faktoren natürlich auch in der Flugplanung mit einbeziehen.
Die gesamte Flugplanung wurde ja bisher nur mit rechtweisenden Kursen erstellt.
Da unser Kompass aber durch Deviation und Deklination nicht immer auf den geographischen Nordpol zeigt müssen auch diese beiden Faktoren noch berücksichtigt werden, damit wir mit dem Kompasssteuerkurs (KSK) auch wirklich ans Ziel kommen.
Die Flugplanung aus 'Flugplanung und Kursberechnung' sollte für den zweiten Streckenabschnitt einen rechtweisenden Steuerkurs von 350° ergeben haben. Wir berechnen jetzt den dazugehörigen KSK.
rwSK: 357°
Ortsmissweisung: 9° West
Korrektur der Ortsmissweisung
Da wir unseren rechtweisenden Steuerkurs berechnet haben können wir daraus, mit
Hilfe der Ortsmissweisung, den missweisenden Steuerkurs ermitteln.
Mit der Ortsmissweisung verhält es ähnlich wie mit dem Windwinkel.
West = Ortsmissweisung negativ, Ost = Ortsmissweisung positiv
Der Rechenweg sieht wie folgt aus:
rwSK - OM = mwSK
Also hier:
350° rwSK - (-9° OM) = 359° mwSK
Korrektur der Deviation
Nun werden wir den Kompass Steuerkurs ermitteln, dazu der Rechenweg:
mwSK + DEV = KSK
Für die Deviation ist der für das jeweilige Flugzeug
zutreffende Wert der Deviationstabelle zu entnehmen
- Real ist die Deviation für jedes Flugzeug anders
- Also auch für unterschiedliche Flugzeuge vom selben Muster
- Nach jeder Reparatur oder Wartung kann sich der Wert ändern
- Auch Waffen- oder Munitionszuladung kann die Deviation verändern
- Deswegen gibt es auch für jede einzelne Maschine
eine eigene Deviationstabelle
- In Simulationen (sofern unterstützt) allerdings meistens nur eine je Muster
In unserem Fall sind es -2°.
Hier erneut die in der kompletten Schulung genutzte Deviationstabelle für die Bf-109
| Kurs nach Karte | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deviation | -2 | -1 | 0 | 2 | 3 | 4 | 4 | 3 | 3 | 2 | 1 | 1 | -1 | -3 | -4 | -3 | -1 | 0 | 0 |
| Kurs nach Karte | 180 | 190 | 200 | 210 | 220 | 230 | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 | 360 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deviation | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 0 | -2 | -3 | -3 | -2 | 0 | 1 | 2 | 1 | -1 | -2 | -2 |
Also hier:
359° mwSK + (-2° DEV) = 357° KSK
Dreh- und Beschleunigungsfehler beim Magnetkompass
Die hier aufgezeigten Fehler vom Magnetkompass treten nicht bei Steig- oder Sinkflügen auf.
Es gibt beschleunigungs- und drehfehlerfreie Kompasse, beispielsweise Modelle der Schweizer Firma Bohli-Magnete oder der deutschen Firma Schanz Feinwerktechnik. Bohli- und Schanz- Kompass sind speziell für Segelflugzeuge entwickelt worden und dort insbesondere für den Einsatz im Wolkenflug. Diese Kompasse haben den Nachteil, dass sie von Hand der Querlage des Flugzeugs angepasst werden müssen. Da der Wolkenflug heute im Segelflug-Wettbewerb
verboten ist, sind sie heute auch in Segelflugzeugen nur noch selten anzutreffen. Außerhalb der
Segelflugszene ist diese Variante des Kompasses kaum bekannt.
Drehfehler
Beim Kurvenflug tritt der Drehfehler auf. Dieser beruht beruht auf der Schräglage des Kompasses in Kurven und tritt in Nord-Süd- Richtung auf. Dabei wird der Kompassmagnet durch die vertikale Komponente des Erdmagnetfeldes verstellt. Eine Kurve ist daher auf nördlichen Kursen früher, auf südlichen später zu beenden, als der Kompass anzeigt.
Dies gilt auf der Nordhalbkugel, auf der Südhalbkugel ist der Effekt entgegengesetzt.
Heute werden im Motorflug Kurven allgemein
nach dem drehfehlerfreien Kurskreisel geflogen, sodass der Kompassdrehfehler hier kaum noch
von praktischer Bedeutung ist.
Beschleunigungsfehler
In der Luftfahrt zeigt der Magnetkompass aufgrund seiner Massenträgheit bei Beschleunigungen falsche Werte an. Er entsteht, weil bei den in der Luftfahrt üblichen Kompassen der Schwerpunkt des drehbaren Teils tiefer liegt als dessen Aufhängepunkt. Bei Beschleunigungen quer zur Magnetisierung (Ost-West-Richtung) kippt der Kompassmagnet derart, dass die vertikale Komponente des Erdmagnetfelds dessen Nordpol nach unten ziehen kann, was die Anzeige verfälscht.
Berechnungen mittels Zusatztabellen
In allen bisherigen Berechnungen (siehe 'Flugplanung und Kursberechnung') haben wir ja fast alles mit dem Dreieckrechner erledigt.
Bei meinem Stöbern in verschiedenen Dokumenten aus der damaligen Zeit bin ich immer wieder auf diverse Zusatztabellen gestoßen, wenn es um die Berechnungen ging.
Luvwinkel und Grundgeschwindigkeit
Für den Luv-Winkel und die Grundgeschwindigkeit gab es für die jeweilige 'Eigengeschwindigkeit' (also Eile) eine Luvwinkel-Tabelle.
Dieses Originaldokument habe ich unter anderem bei 'deutscheluftwaffe.de' gefunden. Zusätzlich sind auf der selben Seite auch noch Umrechnungstabellen für Entfernungen (Flugstrecke) bei Geschwindigkeiten (Fahrt über Grund) und Zeiten (Flugdauer) sowie die Umrechnung diverser Maßeinheiten für Windgeschwindigkeiten (Beaufort - m/s - km/h) und Entfernungen (km - sm) zu finden.
| Luvwinkel-Tabelle | Eigengeschwindigkeit 360 km/h | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WW Windrichtung zum Grundkurs von vorn ° |
Windstärke in km/h | WW Windrichtung zum Grundkurs von vorn ° |
|||||||||||||
| 7 | 14 | 22 | 29 | 36 | 43 | 50 | 58 | 65 | 72 | 79 | 86 | 94 | 101 | ||
| LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
||
| 0 | 0 353 |
0 346 |
0 338 |
0 331 |
0 324 |
0 317 |
0 310 |
0 302 |
0 295 |
0 288 |
0 281 |
0 274 |
0 266 |
0 259 |
0 |
| 15 | 0 353 |
1 346 |
1 339 |
1 332 |
1 325 |
2 318 |
2 311 |
2 304 |
3 297 |
3 290 |
3 283 |
4 276 |
4 269 |
4 262 |
15 |
| 30 | 0 354 |
1 347 |
1 341 |
1 335 |
1 328 |
2 322 |
2 315 |
2 308 |
3 312 |
3 296 |
3 289 |
4 283 |
4 276 |
4 269 |
30 |
| 45 | 1 355 |
1 350 |
2 344 |
2 339 |
3 334 |
3 328 |
4 323 |
5 317 |
5 311 |
6 306 |
6 300 |
7 394 |
7 288 |
8 282 |
45 |
| 60 | 1 356 |
2 353 |
3 349 |
4 345 |
5 341 |
6 337 |
7 332 |
8 328 |
9 323 |
10 319 |
11 314 |
12 309 |
13 304 |
14 299 |
60 |
| 75 | 1 358 |
2 356 |
3 354 |
4 352 |
6 349 |
7 346 |
8 344 |
10 341 |
11 338 |
12 335 |
13 331 |
14 328 |
15 324 |
16 321 |
75 |
| 90 | 1 360 |
2 360 |
3 359 |
5 359 |
6 358 |
7 357 |
8 356 |
9 355 |
10 354 |
12 353 |
13 351 |
14 350 |
15 348 |
16 346 |
90 |
| 105 | 1 363 |
2 364 |
3 365 |
4 366 |
6 368 |
7 369 |
8 370 |
9 371 |
10 371 |
11 372 |
12 372 |
13 373 |
15 373 |
16 373 |
105 |
| 120 | 1 363 |
2 364 |
3 365 |
4 366 |
5 368 |
6 369 |
7 370 |
8 371 |
9 371 |
10 372 |
11 372 |
12 373 |
13 373 |
14 373 |
120 |
| 135 | 1 365 |
2 370 |
2 375 |
3 380 |
4 385 |
5 389 |
6 394 |
7 398 |
7 403 |
8 407 |
9 412 |
10 416 |
11 420 |
11 424 |
135 |
| 150 | 1 366 |
1 373 |
2 379 |
2 385 |
3 391 |
3 397 |
4 403 |
5 409 |
5 415 |
6 421 |
6 426 |
7 432 |
7 438 |
8 444 |
150 |
| 165 | 0 367 |
1 374 |
1 381 |
1 388 |
1 395 |
2 402 |
2 409 |
2 415 |
3 422 |
3 429 |
3 436 |
4 443 |
4 450 |
4 456 |
165 |
| 180 | 0 367 |
0 374 |
0 382 |
0 389 |
0 396 |
0 403 |
0 410 |
0 418 |
0 425 |
0 432 |
0 439 |
0 446 |
0 454 |
0 | 180 |
Fahrt über Grund
Und für die 'wahre Eigengeschwindigkeit' (oder um in unseren Begriffen zu bleiben die 'Fahrt über Grund') den Nav. Vordruck K14 in verschiedenen Ausführungen.
Diesen gab es als K14 S mit Angaben in Seemeilen/h (also Knoten) für die Seeflieger und als K14 L in km/h für alle übrigen Fliegerverbände.
Im Jahr 1940 wurden beide zusammengefasst in den K14, weil auch die Seeflieger der Luftwaffe unterstellt wurden.
Benutzt wurde er um die Abweichung des Fahrtmessers (also die fehlerhafte Anzeige der Eile) durch Temperatur und Flughöhe auszugleichen.
Ich beziehe ich im gesamten weiteren Verlauf auf den Vordruck K14 L aus dem Jahr 1939, da er (zumindest in 'Cliffs of Dover') am besten passt.
Auch dieses Originaldokument habe ich unter anderem bei 'deutscheluftwaffe.de' gefunden
| Tafel II, Leitzahlen | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Höhe über See in km |
Verb. Außentemp. in Flughöhe °C | ||||||||
| -50 | -40 | -30 | -20 | -10 | 0 | 10 | 20 | 30 | |
| 0 | -8 | -6 | -4 | -3 | -1 | 1 | 3 | ||
| 0,5 | -7 | -5 | -3 | -2 | 0 | 2 | 4 | 6 | |
| 1 | -7 | -4 | -2 | 0 | 1 | 3 | 5 | 7 | 9 |
| 1,5 | -4 | -1 | 1 | 3 | 5 | 7 | 9 | 10 | 12 |
| 2 | -1 | 4 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| 2,5 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 |
| 3 | 6 | 8 | 10 | 13 | 15 | 17 | 19 | 21 | 23 |
| 3,5 | 9 | 12 | 14 | 16 | 19 | 21 | 23 | 25 | 27 |
| 4 | 13 | 15 | 18 | 20 | 23 | 25 | 27 | 29 | 32 |
| 4,5 | 17 | 19 | 22 | 24 | 27 | 29 | 31 | 34 | 36 |
| 5 | 21 | 23 | 26 | 28 | 31 | 33 | 36 | 38 | 40 |
| 5,5 | 25 | 27 | 30 | 33 | 35 | 38 | 40 | 43 | 45 |
| 6 | 29 | 32 | 35 | 37 | 40 | 43 | 45 | 48 | 50 |
| 6,5 | 34 | 36 | 39 | 42 | 45 | 48 | 50 | 53 | 56 |
| 7 | 38 | 41 | 44 | 47 | 50 | 53 | 56 | 58 | |
| 7,5 | 43 | 50 | 53 | 56 | 58 | ||||
| 8 | 48 | 52 | 55 | 58 | |||||
| 8,5 | 54 | 57 | |||||||
| 9 | 60 | ||||||||
| Tafel III | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Berichtigte Fartmessanzeige in km/h | |||||||||||||||||||||
| 310 | 320 | 330 | 340 | 350 | 360 | 370 | 380 | 390 | 400 | 410 | 420 | 430 | 440 | 450 | 460 | 470 | 480 | 490 | 500 | ||
| Leitzahl | Wahre Eigengeschwindigkeit in km/h | Leitzahl | |||||||||||||||||||
| -8 | 283 | 292 | 302 | 311 | 320 | 328 | 337 | 346 | 355 | 363 | 272 | 381 | 390 | 398 | 407 | 416 | 425 | 433 | 442 | 451 | -8 |
| -6 | 289 | 299 | 308 | 318 | 326 | 335 | 344 | 353 | 362 | 371 | 380 | 389 | 398 | 407 | 416 | 425 | 434 | 442 | 451 | 460 | -6 |
| -4 | 296 | 305 | 314 | 323 | 333 | 342 | 351 | 360 | 369 | 379 | 388 | 397 | 406 | 415 | 424 | 434 | 441 | 453 | 446 | 470 | -4 |
| -2 | 302 | 312 | 321 | 330 | 340 | 349 | 358 | 367 | 377 | 386 | 396 | 405 | 414 | 423 | 433 | 442 | 452 | 460 | 470 | 479 | -2 |
| 0 | 308 | 318 | 327 | 337 | 346 | 356 | 365 | 375 | 384 | 394 | 403 | 413 | 422 | 432 | 441 | 451 | 460 | 470 | 479 | 489 | 0 |
| 2 | 314 | 323 | 334 | 343 | 353 | 362 | 372 | 382 | 392 | 401 | 411 | 420 | 430 | 440 | 450 | 460 | 469 | 479 | 489 | 499 | 2 |
| 4 | 320 | 330 | 340 | 350 | 360 | 369 | 379 | 389 | 399 | 409 | 419 | 429 | 438 | 449 | 458 | 468 | 478 | 488 | 498 | 508 | 4 |
| 6 | 326 | 336 | 346 | 356 | 366 | 377 | 388 | 397 | 407 | 417 | 427 | 437 | 447 | 457 | 467 | 477 | 487 | 497 | 507 | 517 | 6 |
| 8 | 332 | 342 | 352 | 362 | 373 | 383 | 393 | 404 | 414 | 424 | 435 | 445 | 455 | 465 | 475 | 486 | 496 | 506 | 516 | 526 | 8 |
| 10 | 338 | 348 | 359 | 369 | 380 | 390 | 400 | 411 | 421 | 432 | 442 | 453 | 463 | 474 | 484 | 494 | 505 | 515 | 525 | 535 | 10 |
| 12 | 343 | 354 | 365 | 376 | 386 | 397 | 407 | 418 | 429 | 439 | 450 | 461 | 471 | 482 | 493 | 503 | 513 | 524 | 534 | 544 | 12 |
| 14 | 349 | 360 | 371 | 382 | 393 | 404 | 414 | 425 | 436 | 447 | 458 | 469 | 479 | 490 | 501 | 512 | 522 | 533 | 543 | 553 | 14 |
| 16 | 356 | 366 | 378 | 388 | 399 | 411 | 421 | 432 | 443 | 455 | 466 | 477 | 488 | 498 | 510 | 521 | 530 | 541 | 551 | 562 | 16 |
| 18 | 361 | 373 | 383 | 396 | 406 | 417 | 428 | 439 | 451 | 462 | 474 | 485 | 496 | 507 | 518 | 529 | 539 | 549 | 560 | 571 | 18 |
| 20 | 367 | 379 | 390 | 401 | 413 | 424 | 435 | 447 | 458 | 470 | 481 | 494 | 504 | 515 | 526 | 537 | 548 | 558 | 569 | 580 | 20 |
| 22 | 373 | 385 | 397 | 408 | 419 | 431 | 442 | 454 | 466 | 477 | 489 | 501 | 512 | 523 | 534 | 545 | 556 | 567 | 578 | 589 | 22 |
| 24 | 379 | 391 | 402 | 414 | 426 | 437 | 449 | 461 | 473 | 485 | 497 | 509 | 520 | 531 | 542 | 553 | 565 | 576 | 587 | 598 | 24 |
| 26 | 385 | 397 | 409 | 420 | 433 | 445 | 456 | 478 | 480 | 493 | 505 | 517 | 528 | 539 | 550 | 562 | 573 | 584 | 595 | 607 | 26 |
| 28 | 391 | 403 | 415 | 427 | 439 | 452 | 463 | 475 | 488 | 500 | 513 | 524 | 535 | 547 | 558 | 570 | 582 | 593 | 604 | 616 | 28 |
| 30 | 397 | 409 | 421 | 434 | 446 | 458 | 470 | 483 | 495 | 508 | 520 | 531 | 543 | 555 | 566 | 578 | 590 | 602 | 613 | 625 | 30 |
| 32 | 402 | 415 | 428 | 440 | 453 | 465 | 477 | 490 | 503 | 515 | 527 | 539 | 551 | 563 | 574 | 586 | 598 | 611 | 622 | 634 | 32 |
| 34 | 408 | 421 | 434 | 446 | 459 | 472 | 485 | 497 | 510 | 522 | 534 | 547 | 559 | 571 | 583 | 594 | 607 | 619 | 631 | 643 | 34 |
| 36 | 414 | 427 | 440 | 452 | 466 | 479 | 492 | 505 | 517 | 530 | 542 | 554 | 567 | 578 | 591 | 603 | 615 | 628 | 640 | 652 | 36 |
| 38 | 420 | 434 | 446 | 458 | 473 | 486 | 499 | 512 | 524 | 536 | 549 | 562 | 574 | 586 | 599 | 611 | 624 | 636 | 648 | 661 | 38 |
| 40 | 426 | 439 | 453 | 465 | 479 | 493 | 506 | 519 | 531 | 544 | 557 | 569 | 582 | 594 | 607 | 620 | 632 | 645 | 657 | 669 | 40 |
| 42 | 432 | 445 | 459 | 472 | 486 | 499 | 513 | 526 | 539 | 551 | 564 | 576 | 590 | 602 | 615 | 628 | 640 | 654 | 666 | 678 | 42 |
| 44 | 438 | 451 | 465 | 478 | 493 | 506 | 520 | 532 | 546 | 558 | 571 | 584 | 597 | 610 | 623 | 635 | 649 | 662 | 674 | 686 | 44 |
| 46 | 444 | 457 | 472 | 484 | 499 | 513 | 526 | 539 | 552 | 566 | 579 | 592 | 605 | 618 | 631 | 645 | 658 | 670 | 682 | 694 | 46 |
| 48 | 450 | 466 | 477 | 491 | 506 | 520 | 533 | 546 | 559 | 573 | 586 | 600 | 612 | 626 | 639 | 653 | 666 | 678 | 690 | 703 | 48 |
| 50 | 455 | 470 | 484 | 498 | 512 | 526 | 539 | 553 | 566 | 580 | 594 | 607 | 620 | 634 | 647 | 661 | 674 | 686 | 699 | 712 | 50 |
| 52 | 461 | 475 | 490 | 505 | 519 | 532 | 546 | 560 | 574 | 587 | 601 | 614 | 628 | 642 | 656 | 669 | 682 | 694 | 707 | 720 | 52 |
| 54 | 467 | 482 | 496 | 512 | 525 | 538 | 553 | 567 | 581 | 594 | 608 | 622 | 636 | 650 | 664 | 676 | 690 | 702 | 716 | 729 | 54 |
| 56 | 473 | 488 | 503 | 517 | 531 | 546 | 559 | 574 | 587 | 602 | 616 | 630 | 644 | 658 | 671 | 684 | 698 | 710 | 725 | 737 | 56 |
| 58 | 479 | 494 | 509 | 523 | 538 | 552 | 566 | 580 | 594 | 609 | 624 | 638 | 651 | 665 | 679 | 692 | 707 | 718 | 732 | 745 | 58 |
| 60 | 485 | 500 | 515 | 530 | 544 | 558 | 573 | 587 | 602 | 616 | 631 | 645 | 659 | 673 | 686 | 700 | 714 | 727 | 740 | 754 | 60 |
Grundgeschwindigkeit
Bisher (siehe 'Flugplanung und Kursberechnung') haben wir uns ja mit dem Dreieckrechner von 'Eile' unter Berücksichtigung von 'Windwinkel' und 'Windgeschwindigkeit' die'Grundgeschwindigkeit' ermittelt.
Das geht mit der Zusatztabelle ein wenig einfacher (wenn auch nicht ganz so genau)
In 'Flugplanung und Kursberechnung' hatten wir ja eine Eile von 360 km/h, einen rechtweisenden Kurs von 308° und Wind aus 255° mit 12 m/s (43 km/h). Also einen Windwinkel von 53° (Links).
Mit diesen Daten haben wir eine Grundgeschwindigkeit von 330 km/h sowie einen Luv-Winkel von 6° ermittelt (reiner Windeinfluss). Anhand des Luv-Winkels haben wir unseren rechtweisenden Steuerkurs von 302° ermittelt.
Wenn ich jetzt in der Tabelle für die Eile von 360 km/h mal nachsehe kommt folgendes heraus:
| Luvwinkel-Tabelle | Eile 360 km/h | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WW Windrichtung zum Grundkurs von vorn ° |
Windstärke in km/h | WW Windrichtung zum Grundkurs von vorn ° |
|||||||||||||
| 7 | 14 | 22 | 29 | 36 | 43 | 50 | 58 | 65 | 72 | 79 | 86 | 94 | 101 | ||
| LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
LW ° GG km/h |
||
| 45 | 1 355 |
1 350 |
2 344 |
2 339 |
3 334 |
3 328 |
4 323 |
5 317 |
5 311 |
6 306 |
6 300 |
7 394 |
7 288 |
8 282 |
45 |
| 60 | 1 356 |
2 353 |
3 349 |
4 345 |
5 341 |
6 337 |
7 332 |
8 328 |
9 323 |
10 319 |
11 314 |
12 309 |
13 304 |
14 299 |
60 |
| 75 | 1 358 |
2 356 |
3 354 |
4 352 |
6 349 |
7 346 |
8 344 |
10 341 |
11 338 |
12 335 |
13 331 |
14 328 |
15 324 |
16 321 |
75 |
Bei einer Windgeschwindigkeit von 43 km/h und einem Windwinkel von 53 ° (Links)
lesen wir einen Luvwinkel von 6 ° sowie eine Grundgeschwindigkeit von 337 km/h ab.
Der Luv-Winkel wird (in Relation zum Windwinkel) immer geringer geändert, wenn man die Daten ansieht. Die Grundgeschwindigkeit hingegen recht konstant. Für den Luv-Winkel wäre also ein Wert zwischen 5 und 6° durchaus passend. Die passende Grundgeschwindigkeit dürfte irgendwo bei 334 bis 335 km/h liegen.
Weiterhin basieren die Daten auf der 'digitalen' (also ungenaueren) Version vom Dreieckrechner. Sofern ich mit den selben Ausgangswerten Daten von einem 'realen' Dreieckrechner habe stelle ich die hier gerne ein (und passe ggf. die Texte an)
Aber trotz allem erstaunlich genau. Vor allem wenn man bedenkt, das die meisten Berechnungen mit dem Dreieckrechner ja mit einer 'Schätzung' der Ergebnisse enden, weil man den Wert zwischen 2 Markierungen nicht wirklich exakt ablesen kann und die hier genutzte 'digitale' Version im Vergleich zur 'realen' Version noch ungenauer ist...
Fahrt über Grund
In allen bisherigen Berechnungen (siehe 'Flugplanung und Kursberechnung') haben wir uns ja mit dem Dreieckrechner von 'Eile' über 'Grundgeschwindigkeit' zu 'Fahrt über Grund' durchgearbeitet.
Das geht mit der Zusatztabelle ein wenig einfacher (wenn auch nicht ganz so genau)
In den Originaldokumenten ist immer von 'Berichtigte Fahrtmessanzeige in km/h' die Rede. Ich nehme für diesen Wert jetzt einfach mal die Grundgeschwindigkeit. Also unsere (immernoch mit dem Dreieckrechner zu ermittelnde) Geschwindigkeit bei Windeinfluss, aber ohne jede Korrektur um Flughöhe oder Temperatur. Und wenn wir keinen Wind haben umso einfacher... Dann ist es ja unsere Eile.
Abgelesen in der Tabelle wird anschliessend die 'Wahre Eigengeschwindigkeit in km/h'. Ich nehme den hier abgelesenen Wert mal als 'Fahrt über Grund'
In 'Flugplanung und Kursberechnung' hatten wir ja eine Eile von 360 km/h, einen rechtweisenden Kurs von 308°, Wind aus 255° mit 12 m/s (43 km/h), Flughöhe 4.500 m und eine Temperatur (in Flughöhe) von -12°C. Mit diesen Daten haben wir eine Grundgeschwindigkeit von 330 km/h ermittelt (reiner Windeinfluss), um anschliessend damit weiterzurechen, und hatten als Endergebnis eine Fahrt über Grund von 413 km/h. Und das alles mit dem 'digitalen' Dreieckrechner...
Wenn ich jetzt in diesen Tabellen mal nachsehe und die 'Berichtigte Fahrtmessanzeige' durch zuvor die ermittelte 'Grundgeschwindigkeit' ersetze kommt folgendes heraus:
| Tafel II, Leitzahlen | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Höhe über NN in km |
Temperatur in °C | ||||||||
| -50 | -40 | -30 | -20 | -10 | 0 | 10 | 20 | 30 | |
| 0 | -8 | -6 | -4 | -3 | -1 | 1 | 3 | ||
| ... | |||||||||
| 4,5 | 17 | 19 | 22 | 24 | 27 | 29 | 31 | 34 | 36 |
| ... | |||||||||
| 9 | 60 | ||||||||
Bei der Temperatur von -12°C (gerundet auf -10°C) in der Flughöhe von 4.500 m haben wir eine Leitzahl von 27.
| Tafel III | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grundgeschwindigkeit in km/h | |||||||||||||||||||||
| 310 | 320 | 330 | 340 | 350 | 360 | 370 | 380 | 390 | 400 | 410 | 420 | 430 | 440 | 450 | 460 | 470 | 480 | 490 | 500 | ||
| Leitzahl | Fahrt über Grund in km/h | Leitzahl | |||||||||||||||||||
| -8 | 283 | 292 | 302 | 311 | 320 | 328 | 337 | 346 | 355 | 363 | 272 | 381 | 390 | 398 | 407 | 416 | 425 | 433 | 442 | 451 | -8 |
| ... | |||||||||||||||||||||
| 26 | 385 | 397 | 409 | 420 | 433 | 445 | 456 | 478 | 480 | 493 | 505 | 517 | 528 | 539 | 550 | 562 | 573 | 584 | 595 | 607 | 26 |
| 28 | 391 | 403 | 415 | 427 | 439 | 452 | 463 | 475 | 488 | 500 | 513 | 524 | 535 | 547 | 558 | 570 | 582 | 593 | 604 | 616 | 28 |
| ... | |||||||||||||||||||||
| 60 | 485 | 500 | 515 | 530 | 544 | 558 | 573 | 587 | 602 | 616 | 631 | 645 | 659 | 673 | 686 | 700 | 714 | 727 | 740 | 754 | 60 |
Bei einer Grundgeschwindigkeit (im Originaldokument 'Berichtigte Fahrtmessanzeige') von 330 km/h
lesen wir bei der Leitzahl von 27 (die es nicht gibt, also nehmen wir die Mittelwerte von 26 und 28) eine Fahrt über Grund (im Originaldokument 'Wahre Eigengeschwindigkeit') von (409 + 415) / 2 = 412 km/h ab.
Erstaunlich genau, vor allem wenn man bedenkt, das die meisten Berechnungen mit dem Dreieckrechner ja mit einer 'Schätzung' der Ergebnisse enden, weil man den Wert zwischen 2 Markierungen nicht wirklich exakt ablesen kann...
Und selbst wenn wir die Daten aus der Tabellenberechnung für die Grundgeschwindigkeit (waren 337, also gerundet 340 km/h) nehmen. Wir liegen nur eine Spalte daneben und wissen trotzdem noch nicht, ob das an unseren 'Ableseschätzungen' oder an der 'Ungenauigkeit' vom digitalen Dreieckrechner liegt. Aber die ermittelten Daten sind immernoch sehr genau. Vermutlich genauer als wir das auch Fliegen können...
Steig- und Sinkflug
In allen bisherigen Berechnungen (siehe 'Flugplanung und Kursberechnung') haben wir unsere Höhe ja konstant gehalten und konnten mit den Ausgangswerten auch vernünftig arbeiten.
Bei Steig- oder Sinkflügen sieht das anders aus. Bestenfalls haben wir immer den selben (oder gar keinen) Wind und das würde dann zumindest die Berechnung des Windeinflusses vereinfachen.
Wir werden aber auf jeden Fall diverse Flughöhen mit unterschiedlichem Luftdruck und unterschiedlichen Temperaturen durchfliegen.
Und welche Faktoren haben beeinflussen unsere Fahrt über Grund bei der Berechnung?
- Wind
- Luftdruck
- Temperatur
Mit der ‚normalen‘ Berechnung mit dem Dreieckrechner kommen wir hier also nicht ans Ziel!
Wir brauchen Durchschnittswerte für die ganze Strecke im Steig- oder Sinkflug.
Ich setze einfach mal fest wir machen einen Steigflug mit einer konstanten Steigrate:
- von 1000m auf 5000m
- rechtweisender Kurs von 215°
- Eile 280 km/h (optimale Steiggeschwindigkeit)
- Vorliegende Wetterdaten:
-- Boden - Temp: 15°C - Wind: 8 m/s aus 65°
-- 1000m - Temp: 9°C - Wind: 8 m/s aus 65°
-- 2000m - Temp: 2°C - Wind: 10 m/s aus 45°
-- 3000m - Temp: -5°C - Wind: 10 m/s aus 45°
-- 4000m - Temp: -12°C - Wind: 10 m/s aus 45°
-- 5000m - Temp: -18°C - Wind: 12 m/s aus 40°
Zuerst berechnen wir den durchschnittlichen Wind:
Summe Windgeschwindigkeit: 8 + 10 + 10 + 10 + 12 m/s = 50 m/s
Summe Windrichtung: 65 + 45 + 45 + 45 + 50° = 250°
Durschnittliche Windgeschwindigkeit: 50 m/s / 5 = 10 m/s
Durschnittliche Windrichtung: 250° / 5 = 50°
Mit diesen Daten ermitteln wir jetzt mit dem Dreieckrechner unsere durchschnittliche Grundgeschwindigkeit von 318 km/h.
| Tafel II, Leitzahlen | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Höhe über NN in km |
Temperatur in °C | ||||||||
| -50 | -40 | -30 | -20 | -10 | 0 | 10 | 20 | 30 | |
| 1 | -7 | -4 | -2 | 0 | 1 | 3 | 5 | 7 | 9 |
| 1,5 | -4 | -1 | 1 | 3 | 5 | 7 | 9 | 10 | 12 |
| 2 | -1 | 4 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| 2,5 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 |
| 3 | 6 | 8 | 10 | 13 | 15 | 17 | 19 | 21 | 23 |
| 3,5 | 9 | 12 | 14 | 16 | 19 | 21 | 23 | 25 | 27 |
| 4 | 13 | 15 | 18 | 20 | 23 | 25 | 27 | 29 | 32 |
| 4,5 | 17 | 19 | 22 | 24 | 27 | 29 | 31 | 34 | 36 |
| 5 | 21 | 23 | 26 | 28 | 31 | 33 | 36 | 38 | 40 |
Als nächstes ermitteln wir die durchschnittliche Leitzahl anhand der Tabelle:
Summe Leitzahlen: 5 + 10 + 15 + 23 + 28 = 81
Durchschnittliche Leitzahl: 81 / 5 = 16 (gerundet)
| Tafel III | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grundgeschwindigkeit in km/h | |||||||||||||||||||||
| 310 | 320 | 330 | 340 | 350 | 360 | 370 | 380 | 390 | 400 | 410 | 420 | 430 | 440 | 450 | 460 | 470 | 480 | 490 | 500 | ||
| Leitzahl | Fahrt über Grund in km/h | Leitzahl | |||||||||||||||||||
| 16 | 356 | 366 | 378 | 388 | 399 | 411 | 421 | 432 | 443 | 455 | 466 | 477 | 488 | 498 | 510 | 521 | 530 | 541 | 551 | 562 | 16 |
Anhand der durchschnittlichen Leitzahl können wir jetzt in der Tabelle die Fahrt über Grund von 366 km/h für die durchschnittliche Grundgeschwindigkeit ablesen. Diese können wir während des gesamten Steigfluges für weitere Berechnungen verwenden.
Dafür fehlt und aber noch ein weiterer Wert. Wie lange der Steigflug dauern wird.
Wie man diesen (und noch viel mehr) mit dem Dreieckrechner herausbekommt steht im 'Zusatzblatt Dreieckrechner'