Blockschulung
Navigationsschule

Thema
Flugplanung und Kursberechnung
Zu einem erfolgreichen Einsatz gehört natürlich auch eine gute Flugplanung. In diesem Teil
werden wir uns deshalb mit der Kursberechnung anhand des Dreieckrechners der Luftwaffe befassen. Dies ist besonders wichtig wenn wir keine, oder nur wenige, Orientierungspunkte ausmachen können, also wenn wir zum Beispiel: Über Wasser, im Tiefflug, Nachts oder durch eine Wolkendecke fliegen. Da das Thema sehr umfangreich und komplex ist, werden wir uns auf das absolute Minimum beschränken, das jeder beherrschen sollte. Daher werden wir Steig- und Sinkflugberechnungen, so wie den Kraftstoffverbrauch und seinen Einfluss außen vor lassen.
Hinweis: Dieser Teil wurde noch komplett mit 'Cliffs of Dover' erstellt.
Die komplette Erstellung und Berechnung eines Flugplanes weist aber nur in wenigen Punkten für 'Battle of Stalingrad' von den Inhalten dieser Schulungseinheit ab.
Zum einen wird für 'Battle of Stalingrad' ein anderes Kartentool genutzt, das nachdem es für einige Zeit gar nicht mehr zur Verfügung stand von findigen Usern reaktiviert wurde und auf einem neuen Server wieder zur Verfügung steht.
Zum anderen werden einige Aspekte der 'normalen' Navigation in 'Battle of Stalingrad' gar nicht simuliert.
Dieses sind die 'Deklination' (Ortsmissweisung) und die 'Deviation' (Kompassabweichung durch Flugzeuginterne Systeme).
Da aber beides erst ganz am Ende der anderen Berechnungen (bei 'Cliffs of Dover' und in der Realität) zusätzlich noch durchgeführt werden muss wird hier ebenfalls darauf eingegangen aber auch entsprechend darauf hingewiesen, das diese Schritte bei 'Battle of Stalingrad' nicht nötig sind.
Für diesen Schulungsteil benötigen wir ausser ein wenig (oder ein wenig mehr...) Zeit und Verständnis noch folgendes:
- Etwas zu schreiben
- Das Kartentool für 'Cliffs of Dover' (Die entsprechende Webseite findet mal hier)
- Einen Dreieckrechner (Die von VO101_Tom erstellte funktionsfähige HTML-Version gibt es auf dieser Seite)
Und da weiter oben ja bereits erwähnt wurde, das für 'Battle of Stalingrad' ein anderes Kartentool benutzt werden muss...
Sowohl für dieses Kartentool, als auch für weitere Funktionen des Dreieckrechners wird der interessierte Leser in späteren Schulungsteilen noch weitere Details finden...
Hier bleiben wie bei dem absolut Nötigen, und auch das ist schon eine ganze Menge an Informationen!
Erklärung der Begriffe
Hier eine grobe Übersicht der genutzten Begriffe, gemäß der Definitionen der Luftwaffe von 1938.
Diverse Bezeichnungen für 'Norden'
rwN - rechtweisend Nord: Geografischer Norden nach Karte
mwN - missweisend Nord: Magnetischer Norden nach Magnetpol
KN - Kompass Nord: Magnetischer Norden mit einbezogener Deviation
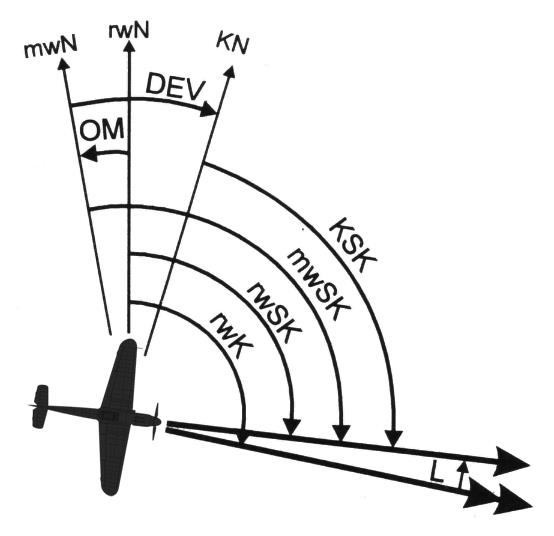
Diverse Bezeichnungen für 'Kurse'
rwK - rechtweisender Kurs: Kurs nach geografischem Norden
rwSK - rechtweisender Steuerkurs: rechtweisender Kurs korrigiert um dem Luv-Winkel
mwSK - missweisender Steuerkurs: rechtweisender Steuerkurs korrigiert um die Missweisung
KSK - Kompass Steuerkurs: Am Kompass abzulesender Kurs nach allen Berechnungen
Diverse Faktoren, die den 'Kompass' direkt beeinflussen
OM - Ortsmissweisung: Siehe "Zusatzblatt Navigation"
DEV - Deviation: Siehe "Zusatzblatt Navigation"
Diverse Winkel und Faktoren, die den 'Kurs' direkt beeinflussen oder für die Berechnung nötig sind
L - Luv-Winkel: Kursdifferenz verursacht durch den Windeinfluss
Abdrift (Lee-Winkel): Verschiebung des rechtweisenden Kurs durch den Windeinfluss
Windwinkel: Einfallwinkel des Windes auf den geplanten rechtweisenden Kurs
Windeinfallwinkel: Einfallwinkel des Windes auf den rechtweisenden Steuerkurs
Windfaktor: Differenz der Fahrt zur Grundgeschwindigkeit verursacht durch den Windeinfluss
Diverse Geschwindigkeiten
Windgeschwindigkeit: Strömungsgeschwindigkeit des Windes
Eigengeschwindigkeit, Fahrt (IAS): Geschwindigkeit relativ zur umgebenden Luftmasse
Grundgeschwindigkeit: Geschwindigkeit relativ zur Luftmasse, abzüglich des Windfaktors
Wahre Geschwindigkeit (TAS): Geschwindigkeit relativ zur Luft mit Korrektur der Druckdifferenz
Fahrt über Grund (GS): Geschwindigkeit relativ zum Boden mit Korrektur der
Druckdifferenz und des Windeinflusses
Sonstige Begriffe
Flugdauer: Benötigte Zeit um einen Wegpunkt zu erreichen, ermittelt durch die Fahrt über Grund
ISA (International Standard Atmosphere): Normatmosphäre = 15 °C/1013 hPa auf Normal-0
WP - Wegpunkt: Für Kurswechsel, Positionskontrolle und nachträgliche Windkorrektur
KwP - Kurswechselpunkt: Zeitpunkt vor dem eigentlichen Wegpunkt, an dem die Kurve eingeleitet wird
Hierzu sei gesagt:
• Rechtweisende (rw) Kurse beziehen sich auf rechtweisend Nord (rwN).
• Alle Arbeiten mit der Karte benutzen immer rechtweisende (rw) Kurse.
• In den Steuerkursen (SK) ist der Luvwinkel (L) enthalten.
• Missweisende (mw) Kurse beziehen sich auf Kompass-Nord (OM enthalten)(mwN).
• Kompasskurse beziehen sich auf Kompass-Nord (OM und DEV enthalten)(KN).
Und um der jetzt auftretenden 'Verzweiflung' durch die Masse an Begriffen direkt entgegenzuwirken:
Und interessiert sobald wir im Flugzeug sitzen nur noch ein Kurs... Der KSK (Kompass Steuerkurs)
und nur noch eine Zeit: Die bis zum nächsten Wegpunkt (oder der nächsten nötigen Aktion wie Kurswechsel, ...)
und beides müssen wir mit den ganzen Werten am Schreibtisch berechnen...
Und mal so als 'Eselsbrücke':
So lange wir in der Karte arbeiten (also auf 'echtem' Papier) benutzen wir auch ausschliesslich die 'echten' (also rechtweisenden) Kurse!
Der Dreieckrechner
Der Dreieckrechner ist ein Rechenschieber mit dem alle wesentlichen Aufgaben der
Kursberechnung gelöst werden können. Somit bildet er, neben der Karte, unser Hauptwerkzeug zur Flugplanung und Kursberechnung.
Digitale Formen sind hier zu finden:
Dreieckrechner DR3 von VO101_Tom als .swf Datei zum Download (benötigt eine installiertes Adobe-Flash) oder als 'HTML-Version'.
Weiterhin eine von JG4_Deciman modifizerte Version (betrifft nur die Optik der Rückseite, und hier genauer gesagt nur der 'Flugzeugscheibe') als .swf-Datei'' (benötigt ebenfalls ein installiertes Adobe-Flash) oder als '.exe-Datei' (läuft somit eigenständig und funktioniert auch mit Windows 10 noch problemlos)
Sein Aufbau erklärt sich wie folgt:
Vorderseite
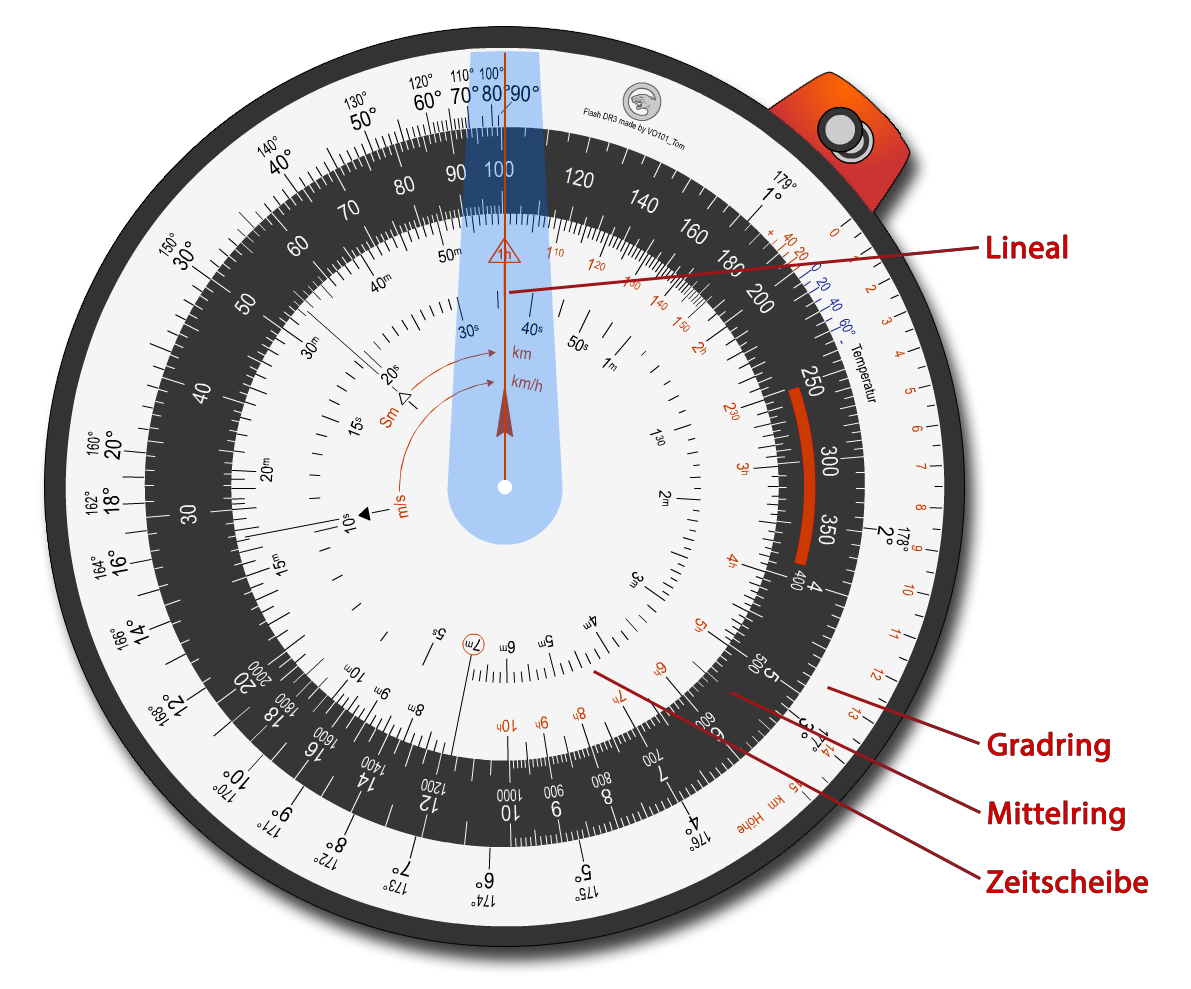
Ausserhalb des runden Dreieckrechners befindet sich eine Schaltfläche, mit der per Mausklick zwischen den beiden Seiten umgeschaltet werden kann. Die Positionen der jeweiligen Bedienelemente der Seite bleiben dabei immer unverändert.
In der Mitte des Dreieckrechners befindet sich ebenfalls eine Schaltfläche. Ein Mausklick auf diese 'verlangsamt' die Drehgeschwindigkeit der einelnen Ringe und des Lineals. Wenn die 'Bremse' aktiv ist wird dies durch einen roten Kreis in der Mitte angezeigt.
Gradring, Mittelring, Zeitscheibe und Lineal können mit der Maus einzeln gedreht werden. Entsprechendes Element mit der Maus erfassen (egal wo), linke Maustaste drücken und gedrückt halten und die Maus bewegen.
Auf der Zeitscheibe befindet sich noch eine weitere Schaltfläche. Der 1-Stunden-Pfeil. In der Grafik etwas oberhalb vom Ende der Linie, die das 'Lineal' markiert, zu sehen.
Diese Schaltfläche hat gleich zwei Funktionen:
Zum einen bringt er bei einem Mausklick darauf das 'Lineal' mit dem '1 Stunden Pfeil' in Deckung.
Zum anderen 'koppelt' der das Lineal (immer in Deckung mit dem '1 Stunden Pfeil') an die Zeitscheibe. In 'gekoppeltem' Zustand wird bei einer Drehung der Zeitscheibe das Lineal mitbewegt. Bewegt man nur das Lineal ist die Koppelung wieder aufgehobwn.
Wenn die Zeitscheibe und Lineal 'gekoppelt' sind hat der '1 Stunden Pfeil' einen roten Hintergrund.
Beide Funktionen werden wir später noch mehrfach nutzen...
Rückseite
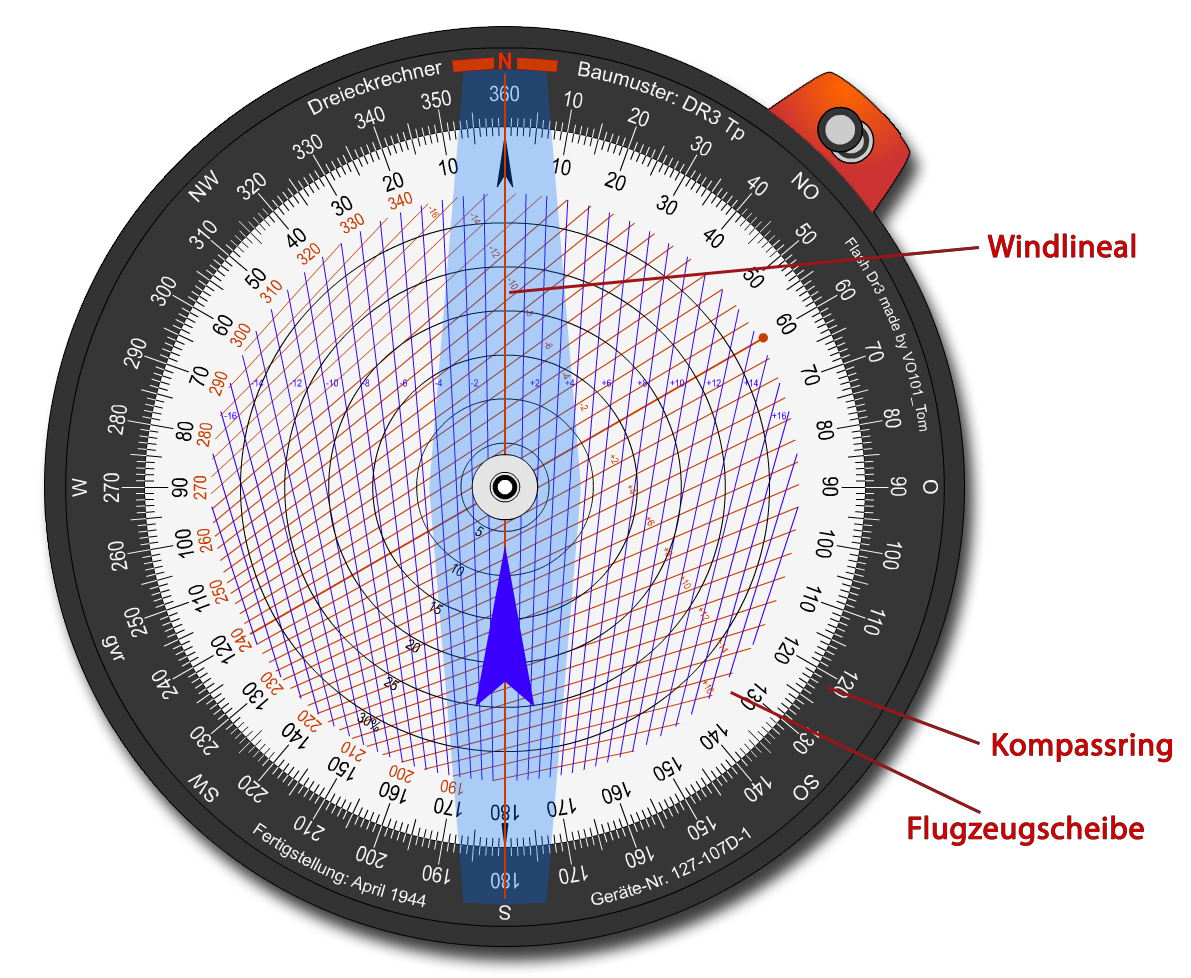
Ausserhalb des runden Dreieckrechners befindet sich auch hier die selbe Schaltfläche, mit der per Mausklick zwischen den beiden Seiten umgeschaltet werden kann. Die Positionen der jeweiligen Bedienelemente der Seite bleiben dabei wieder unverändert.
In der Mitte des Dreieckrechners befindet sich ebenfalls die Schaltfläche zum 'verlangsamen' der Drehgeschwindigkeit der einelnen Ringe und des Lineals. Auch hier wird die aktive 'Bremse' wieder duch einen roten Kreis in der Mitte angezeigt.
Kompassring, Flugzeugscheibe und Windlineal können wieder mit der Maus einzeln gedreht werden. Die Bedienung ist identisch zur Vorderseite.
Hinweis:
Der 'digitale' Dreieckrechner läßt uns zwar die ganzen Berechnungen durchführen (und liefert auch absolut nutzbare und brauchbare Ergenisse), aber er ist nicht so genau, wie die 'Hardware' von 1939. Sollte jemand also einen 'realen' DR2 oder DR3 besitzen und die selben Berechungen damit machen, so wird er ein leicht anderes (und auch genaueres!) Ergebnis bekommen.
Flugplanung
Um einen militärischen Flug gut zu Planen, muss man sich immer der strategischen und
taktischen Gesamtsituation bewusst sein. Das bedeutet: Wir müssen uns bewusst sein wie der Feind aufgestellt ist, wo und in welcher Stärke mit Flugabwehr zu rechnen ist, wann und wo mit Feindflugzeugen, in welcher Stärke, zu rechnen ist und wie ich den Feind am besten täuschen und umgehen, oder in eine Falle locken kann.
Man sollte seinen Plan immer mit anderen verbündeten Einheiten absprechen und gegebenenfalls auch mit diesen koordinieren.
Für die Planung benötigen wir:
• Flugparameter unseres Flugzeugtyps
• Möglichst genaue Wetterdaten
• Einen Abflugpunkt
• Kontrollwegpunkte zur möglichen Kurs- und Windkorrektur
• Sammelräume
• Rückzugsräume
• Ausweichkurse
Doch behaltet immer im Hinterkopf:
Selbst der beste Plan funktioniert nur bis zum ersten Feindkontakt!
Kurs in der Karte eintragen
Zuerst müssen wir geplanten unseren Flug in der Karte eintragen. Hierzu wird im entsprechenden Kartentool ein neuer Flugplan erstellt, in dem dann die einzelnen Wegpunkte eingetragen werden.
Dabei gilt es einen wichtigen Punkt zu beachten:
Um unseren Kurs zu wechseln müssen wir eine Kurve fliegen, und die dafür benötigte Zeit später ebenfalls berechnen und in den Flugplan einbeziehen. Die Differenz zwischen 2 Kursen darf 90° nicht überschreiten. Wollen wir unseren Kurs um mehr verändern müssen wir dieses auf 2 einzelne Kurse verteilen.
Für die Planung in diesem Schulungsteil verwenden wir das HTML-Kartentool für 'Cliffs of Dover'.
Hier haben wir die gesamte Kanalkarte von Cliffs of Dover zu Verfügung und können
Wegpunkte, Flugkurse, Ziele, Besonderheiten, Wind und die Eile über Grund Eintragen.
Für 'Battle of Stalingrad' existiert ein anderes Kartentool, das sich in Aussehen und Bedienung unterscheidet.
Es bietet uns aber die selben Funktionen und Informationen und wird in einem weiteren Schulungsteil noch genauer erklärt.
Mit der ersten Schaltfläche, oben rechts, tragen wir nacheinander die Wegpunkte ein.

Der integrierte Kursrechner spuckt uns dann bereits erste Daten aus.
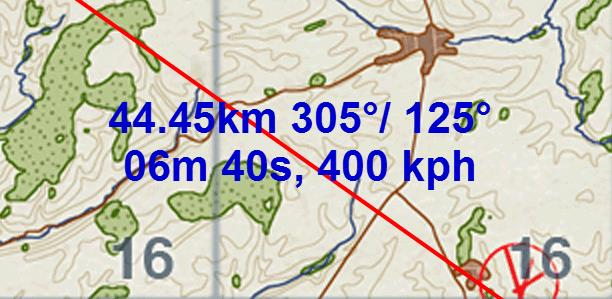
Hier haben wir immer zum nächsten Wegpunkt:
Die Entfernung, den Kurs und Gegenkurs nach rechtweisend Nord und die Flugzeit nach zuvor eingetragener Fahrt über Grund.
Für unsere Berechnungen interessiert uns erst einmal nur die Entfernung und der Kurs.
Die beiden Daten aus der unteren Zeile werden durch den Windeinfluss sowie die für einen Kurswechsel benötigte Zeit irrelevant.
Ich habe hier mal einen Abflugpunkt und zwei weitere Wegpunkte eingetragen:
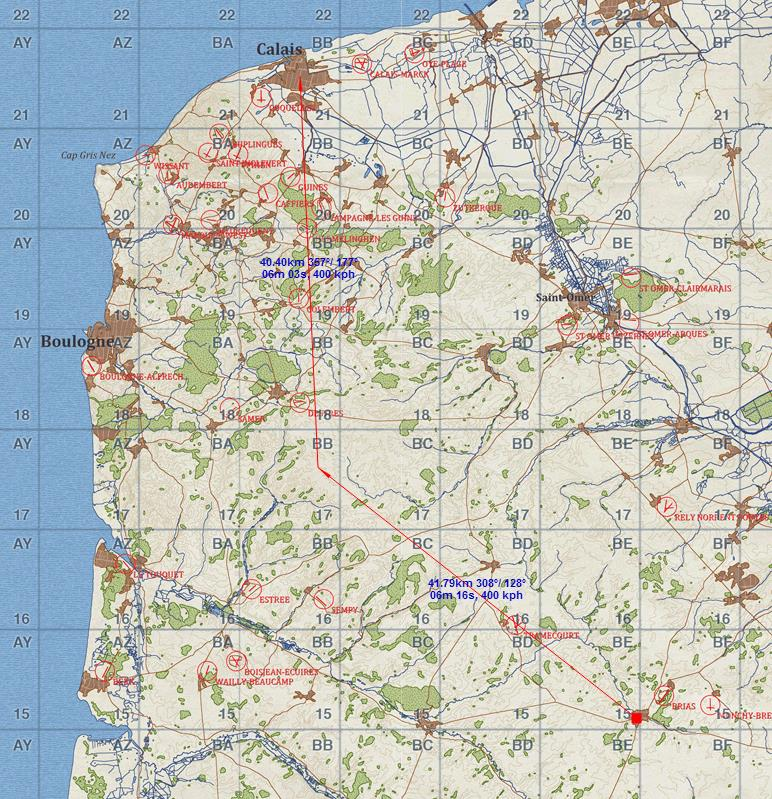
Wir fliegen also, nach Plan, von St. Pot (BE 15-3), über BB 17-6, nach Calais (BB 21-5).
Wenn wir nun mit diesen Informationen losfliegen, wird das Problem sein, dass wir dort niemals ankommen werden wenn wir nach den vorliegenden Daten fliegen. Daher kommen wir nun zur Kursberechnung mit dem Dreieckrechner.
Kursberechnung
Die Kursberechnung wird in den folgenden Schritten durchgeführt:
1. Windwinkel bestimmen
2. Luv-Winkel und Windgeschwindigkeit in km/h bestimmen
3. Windeinfallwinkel und rechtweisenden Steuerkurs bestimmen
4. Grundgeschwindigkeit bestimmen
5. Fahrt über Grund ermitteln
6. Flugdauer bestimmen
7. Kompass-Steuerkurs bestimmen
Bevor wir anfangen, müssen wir allerdings ein paar Daten kennen:
Grunddaten:
Ortsmissweisung: 9° West (aus der Karte entnommen)
Wind: 12 m/s aus 255° (Wetterbericht)
Temperatur am Boden: 15°C (Wetterbericht)
Zum ersten Wegpunkt:
rwK: 308° (laut Karte)
Eile: 360 km/h (geplante Gewschwindigkeit laut Fahrtmesser)
Flughöhe: 4.500 m (geplante Flughöhe)
Entfernung: 41,79 km (laut Karte)
Diese können wir schon einmal in die Kursberechnungstabelle die eintragen. In den weiteren Schritten werden wir mit dem Dreieckrechner die nötigen Werte, also unseren im Flug zu benutzenden Kompas-Steuerkurs sowie die Fahrt über Grund und die daraus resultiernde Flugdauer ermitteln und ebenfalls eintragen.
Und am Ende der ganzen Berechnungen haben wir alle Daten, die uns im Flugzeug auch wirklich von A nach B bringen.
Alle nötigen Werte bis einschliesslich der Bestimmung der Grundgeschwindigkeit können auf verschiedene Arten ermittelt werden:
- mit dem Dreieckrechner
- zeichnerisch mit einem Winddreieck
- rechnerisch im Sinussatz
Windwinkel
| Vorhandene Daten | |
|---|---|
| Wegpunkt | BB 17-6 |
| Windrichtung | 255° |
| Windwinkel | --- |
| Luv-Winkel | --- |
| Windeinfallwinkel | --- |
| Windgeschwindigkeit | 12 m/s |
| Ortsmissweisung | 9° W |
| Deviation | --- |
| rwK | 308° |
| rwSK | --- |
| mwSK | --- |
| KSK | --- |
| Temperatur am Boden | 15°C |
| Außentemperatur in Flughöhe | --- |
| Eile | 360 km/h |
| Grundgeschwindigkeit | --- |
| Fahrt über Grund | --- |
| Flughöhe | 4.500 m |
| Entfernung | 41,79 km |
| Flugdauer | --- |
Mit dem Dreieckrechner bestimmen wir zunächst den Windwinkel.
Hierzu stellen wir auf der
Rückseite des Dreieckrechners die Flugzeugscheibe auf den geplanten rechtweisenden Kurs von
308° und das Windlineal auf die uns bekannte Windrichtung von 255°.
Hinweis: Der Wind kann in verschiedenen Höhen aus verschiedenen Richtumen kommen und auch verschieden stark sein. Wir nehmen die für unsere Flughöhe passenden Daten. In 'Battle of Stalingrad' gelten die Windangaben immer ab der angegebenen Höhe nach oben, bis eine neue Angabe erfolgt.
Der blaue Pfeil des Windlineals gibt hierbei die Windrichtung an.
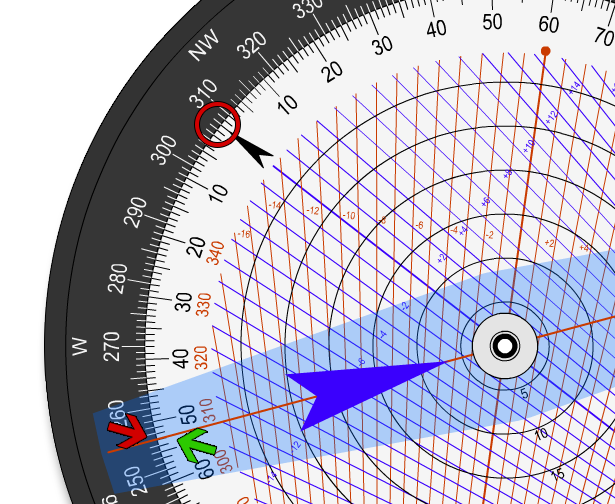
So erhalten wir, über das Windlineal, auf der Flugzeugscheibe den Windwinkel von 53° Links zu
unserem Kurs. Diesen ersten ermittelten Wert können wir jetzt in der Kursberechnungstabelle eintragen.
Luv-Winkel und Windgeschwindigkeit in km/h
| Vorhandene Daten | |
|---|---|
| Wegpunkt | BB 17-6 |
| Windrichtung | 255° |
| Windwinkel | 53° Links |
| Luv-Winkel | --- |
| Windeinfallwinkel | --- |
| Windgeschwindigkeit | 12 m/s |
| Ortsmissweisung | 9° W |
| Deviation | --- |
| rwK | 308° |
| rwSK | --- |
| mwSK | --- |
| KSK | --- |
| Temperatur am Boden | 15°C |
| Außentemperatur in Flughöhe | --- |
| Eile | 360 km/h |
| Grundgeschwindigkeit | --- |
| Fahrt über Grund | --- |
| Flughöhe | 4.500 m |
| Entfernung | 41,79 km |
| Flugdauer | --- |
Als nächstes ermitteln wir den Luv-Winkel und können dabei auch gleich die Windgeschwindigkeit in km/h ablesen.
Hierzu wechseln wir auf die Vorderseite des Dreieckrechners.

Hier stellen wir nun mit dem Gradring den ermittelten
Windwinkel von 53° auf die zuvor festgelegte Eile von
360 km/h auf dem Mittelring.
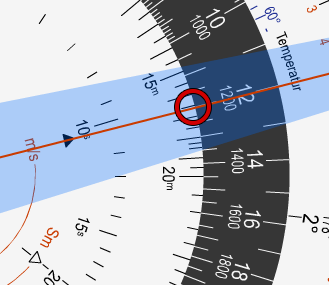
Anschließend stellen wir mit der Zeitscheibe den m/s-Pfeil auf die uns bekannte Windgeschwindigkeit von 12 m/s auf dem Mittelring, hierbei können wir das Lineal zur Hilfe nehmen.
Auch hier wieder die Angabe der Windstärke für unsere Flughöhe verwenden.
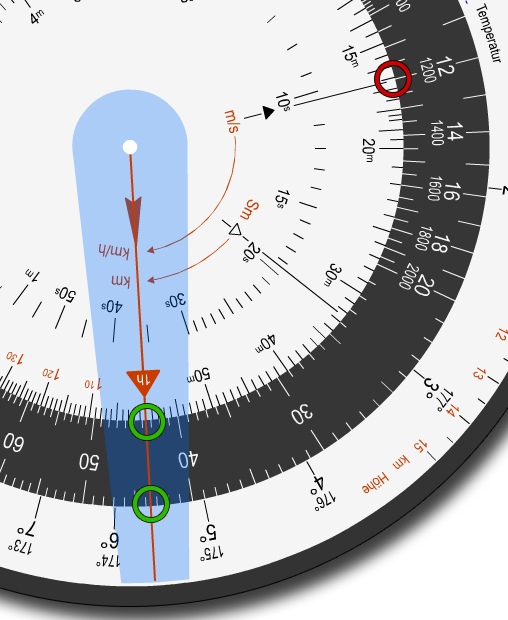
Nun können wir mit einem Klick auf den 1h-
Pfeil der Zeitscheibe, das Lineal auf diesem
fixieren.
Somit erhalten wir zum einen, auf
dem Mittelring die Windgeschwindigkeit in
km/h (hier ungefähr 43 km/h), als auch auf dem Gradring den Luv-
Winkel von ungefähr 5,6°.
Nun können wir versuchen diese Zahl so weiter zu verwenden, oder wir runden diese zur
Vereinfachung, also beträgt der Luv-Winkel 6°.
Diese beiden Werte können wir jetzt ebenfalls in die Kursberechnungstabelle eintragen.
Noch ein wichtiger Hinweis:
Damit der Wind uns auch vom Kurs abbringt muss er auch in einem gewissen Maße seitlich auf das Flugzeug treffen. Bei nahezu Rücken- oder Gegenwind wird unser Kurs nicht beeinflusst. Hier müssen wir lediglich die geplante Eile anhand der Windgeschwindigkeit korrigieren und als Grundgeschwindigkeit in die weiteren Berechnungen übernehmen.
Bei der hier verwendeten Windgeschwindigkeit von 12 m/s (oder 43 km/h) und der geplanten Eile von 360 km/h wird sich unsere Grundgeschwindigkeit bei Gegenwind um die Windgeschwindigkeit verlangsamen, aber bei Rückenwind in selbem Maße steigen.
Einen Luv-Winkel von 1° (und somit eine leichte Kursabweichung) erreichen wir hier aber erst, wenn der Windwinkel 8° beträgt.
Windeinfallwinkel
| Vorhandene Daten | |
|---|---|
| Wegpunkt | BB 17-6 |
| Windrichtung | 255° |
| Windwinkel | 53° Links |
| Luv-Winkel | 6° |
| Windeinfallwinkel | --- |
| Windgeschwindigkeit |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W |
| Deviation | --- |
| rwK | 308° |
| rwSK | --- |
| mwSK | --- |
| KSK | --- |
| Temperatur am Boden | 15°C |
| Außentemperatur in Flughöhe | --- |
| Eile | 360 km/h |
| Grundgeschwindigkeit | --- |
| Fahrt über Grund | --- |
| Flughöhe | 4.500 m |
| Entfernung | 41,79 km |
| Flugdauer | --- |
Jetzt ermitteln wir den Windeinfallwinkel.
Wir gehen wieder auf die Rückseite des Dreieckrechners.
Jetzt ist es wichtig darauf zu achten ob der Windwinkel links oder rechts zum Kurs ist, hier gilt:
Links = Luv-Winkel subtrahieren
Rechts = Luv- Winkel addieren
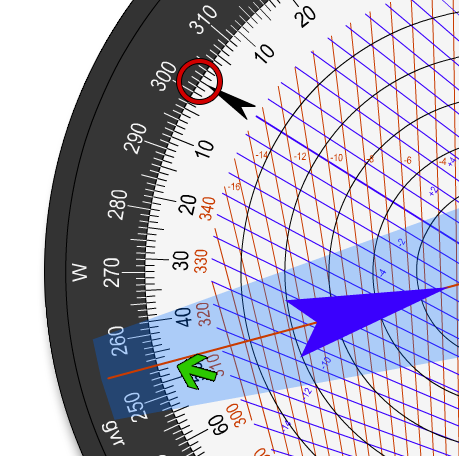
Da unser Windwinkel links ist subtrahieren wir den Luv-Winkel von unserem rechtweisenden Kurs, und erhalten so unseren rechtweisenden Steuerkurs, also:
308° rwK - 6° L = 302° rwSK
Jetzt stellen wir mit der Flugzeugscheibe den berechneten rwSK von 302° ein.
Dadurch erhalten wir über das unveränderte
Windlineal den Windeinfallwinkel, in diesem Fall von 47°.
Die gewonnenen Daten (Windwinkel und rwSK) können wir wieder in die Kursberechnungstabelle eintragen.
Grundgeschwindigkeit
| Vorhandene Daten | |
|---|---|
| Wegpunkt | BB 17-6 |
| Windrichtung | 255° |
| Windwinkel | 53° Links |
| Luv-Winkel | 6° |
| Windeinfallwinkel | 47° |
| Windgeschwindigkeit |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W |
| Deviation | --- |
| rwK | 308° |
| rwSK | 302° |
| mwSK | --- |
| KSK | --- |
| Temperatur am Boden | 15°C |
| Außentemperatur in Flughöhe | --- |
| Eile | 360 km/h |
| Grundgeschwindigkeit | --- |
| Fahrt über Grund | --- |
| Flughöhe | 4.500 m |
| Entfernung | 41,79 km |
| Flugdauer | --- |
Jetzt ermitteln wir die Grundgeschwindigkeit und kennen zusätzlich noch den Windfaktor, die Differenz zwischen Eile und Grundgeschwindigkeit.
Hierzu wechseln wir auf die unveränderte Vorderseite des Dreieckrechners.
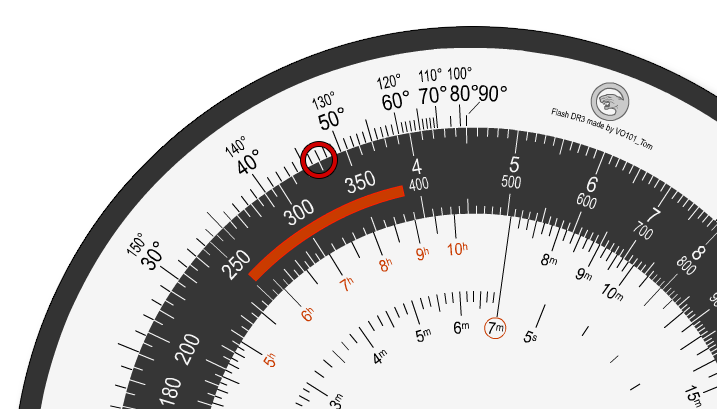
Anhand des ermittelten Windeinfallwinkels von 47° auf dem Gradring können wir jetzt auf dem Mittelring die Grundgeschwindigkeit von 330 km/h ablesen.
Außerdem ist und nun der Windfaktor von 30 km/h als Differenz zwischen Eile und Grundgeschwindigkeit bekannt.
Die Grundgeschwindigkeit können wir wieder in die Kursberechnungstabelle eintragen.
Zeichnerischer Weg
Alles nötigen Werte, die wir bisher mit dem Dreieckrechner berechnet haben (Luv-Winkel, rechtweisenden Steuerkurs und Grundgeschwindigkeit) kann man auf der Karte auch zeichnerisch ermitteln
Für das folgende Beispiel nehmen wir einfach mal an, das der Maßstab unserer Karte für uns genau passend genau für die Entfernung von 360 km für einen geplanten Kurs vom Startpunkt zum Zielpunkt übereinstimmt, und somit 360 mm lang ist (1 mm/km). Weiterhin nehmen wir mal an, das unsere geplante Strecke genau 360 km ist. Die rot eingezeichnete Strecke (geplanter Kurs) würde also auf der Karte genau 360 mm lang sein, weil wir bei einer geplanten Eile von 360 km/h genau eine Stunde dafür brauchen würden. Und diese eine Stunde auf dem Kurs ist wichtig um den Wind passend einzuzeichnen.
Hinweis: Man kann alle Linien auf der Karte auch auf andere 'unpassende' Maßstäbe oder sogar Flugzeiten anwenden. Dann muss man sie halt nach beim Einzeichnen oder Ausmessen entsprechend mit den entsprechenden Faktoren multiplizieren.
Unseren geplanten (rechtweisenden) Kurs kennen wir.
Die Windrichtung und Windgeschwindigkeit ebenfalls.
Sofern die Windgeschwindigkeit in m/s angegeben wurde müssen wir umrechnen. Entweder wie unter anderem auf der Seite 'Luv-Winkel und Windgeschwindigkeit in km/h' beschrieben wurde mit dem Dreieckrechner, oder wir nehmen die multiplizieren die Angabe in m/s mit 3,6 und erhalten die nötigen km/h.
Jetzt zeichnen wir auf der Karte unseren rechtweisenden Kurs von 308° vom Startpunkt zum Zielpunkt ein. Diese Linie wird durch die 'angenommenen' Bedingungen auch genau 360 mm lang sein.
Am Zielpunkt zeichnen wir eine Linie für den 'Gegenkurs' der Windrichtung in der passenden Länge für die Windgeschwindigkeit in km/h ein. Im aktuellen Beispiel sind das 43mm in Richtung 75°. Diese Linie ist die Windreferenz. Der Punkt am Ende der Linie ist unser Windreferenzpunkt. An genau diesem Punkt werden wir nach der vorgesehenen Flugzeit laden wenn wir nicht auf den Wind reagieren und unsere geplante Geschwindigkeit beibehalten.
Eine weitere Linie vom Zielpunkt wird für die Windrichtung in der passenden Länge für die Windgeschwindigkeit in km/h ein. Im aktuellen Beispiel sind das 43mm in Richtung 255°. Diese Linie ist der Windübertrag. Der Punkt am Ende der Linie ist unser Windübertragspunkt. Auf genau diesen Punkt müssen wir zusteuern und unsere Geschwindigkeit anpassen, wenn wir den geplanten Zielpunkt nach der vorgesehenen Flugzeit erreichen wollen.
Jetzt zeichnen wir weitere Linien ein.
Eine Driftlinie vom Startpunkt zum Windreferenzpunkt und eine Steuerlinie vom Startpunkt zum Windübertragspunkt.
Das Ergebnis sieht dann auf der Karte so aus
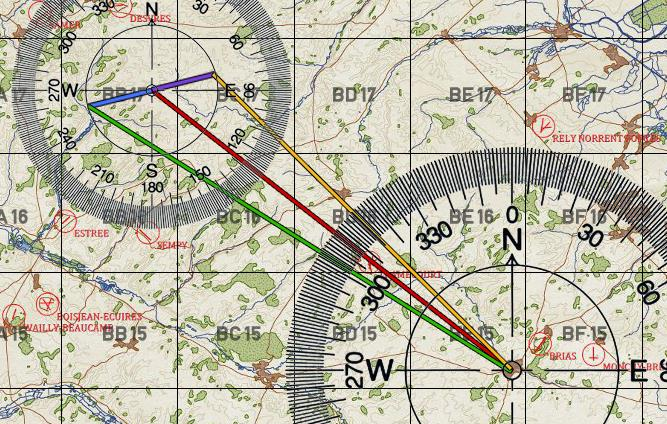
Aus den eingezeichneten Linien können wir folgendes ablesen:
Welchen Kurs (und welche Eile) wir fliegen müssten, um den Zielpunkt nach einer Stunde zu Erreichen
(Länge und Richtung der Steuerlinie mit Windübertragspunkt am Ende)
Wo wir landen wenn wir nicht reagieren und Kurs und Geschwindgkeit nicht anpassen
(Driftlinie mit Windreferenzpunkt als Ende)
Wir wollen aber unsere geplante Geschwindigkeit nicht bei jedem Kurswechsel anpassen, sondern sie beibehalten.
Also 'mischen' wir die zeichnerisch ermittelten Werte:
Die 'Länge' der Driftlinie (sollten 330 mm sein) ergibt unsere Grundgeschwindigkeit (also 330 km/h)
und die 'Richtung' der Steuerlinie (sollten 302° sein) ergibt unseren rechtweisenden Steuerkurs.
Die Flugdauer wird sich dadurch ändern, aber diese wird ja erst später anhand der ermittelten Grundgeschwindigkeit, Entfernung und weiterer Faktoren berechnet.
Zusätzlich können wir auch unseren Luv-Winkel (Winkeldifferenz zwischen rechtweisendem Kurs und Steuerlinie) von 6° Links (weil kleiner) sowie unseren Lee-Winkel (Winkeldifferenz zwischen rechtweisendem Kurs und Driftlinie) von 5° Rechts (weil größer)) ablesen
Rechnerischer Weg
Fast alle bisher mit dem Dreieckrechner durchgeführten Berechnungen basieren auf dem Sinussatz und lassen sich auch rein mathematisch lösen...
Die bekannten Werte oder vorab zu errechnenden Werte sowie die weiteren dadurch im Sinussatz berechenbaren Werte sind in den Formeln gekennzeichnet.
Alle Werte im Sinussatz
| 𝑠𝑖𝑛 𝐿𝑢𝑣-W𝑖𝑛𝑘𝑒𝑙 | = | sin Windwinkel | = | sin Windeinfallwinkel |
| Windgeschwindigkeit in km/h | Eile | Grundgeschwindigkeit |
| 𝑠𝑖𝑛 5,6° | = | sin 53° | = | sin 47° |
| 43 km/h | 360 km/h | 330 km/h |
Windgeschwindigkeit in km/h
Windgeschwindigkeit in km/h = Windgeschwindigkeit in m/s * 3,6
43 km/h = 12 m/s * 3,6
Windwinkel
Windwinkel = Windrichtung - rechtweisender Kurs
Hier muss das Ergebnis aber ggf. nochmal modifiziert werden.
Gültige Werte liegen zwischen -180 und 180.
Bei Werten < -180 müssen wir 360 addieren,
bei Werten > 180 müssen wir 360 abziehen.
Das 'Vorzeichen' des Ergebnisses wird in den weiteren Berechnungen weggelassen (der Windwinkel ist also immer positiv).
Es gibt uns aber an, ob der Wind von Links (negatives Vorzeichen) oder Rechts kommt. Weiterhin wird das Vorzeichen in den weiteren Formeln auf den Luv-Winkel übertragen. Wind von Links = negativer Luv-Winkel.
minus 53° = 255° - 308°
Also ein Windwinkel von 53°, Wind von Links und ein negativer Luv-Winkel
Luv-Winkel (Notwendige Kursanpassung in Grad)
In welche Richtung wir unseren Kurs anpassen müssen ergibt sich aus der Berechnung des Windwinkels. Ist das Vorzeichen 'negativ' haben wir Wind von Links, und müssen unseren Kurs also um die errechnete Gradzahl nach links anpassen (also vom rechtweisenden Kurs abziehen).
| sin Luv-Winkel = | Windgeschwindigkeit in km/h | * sin Windwinkel |
| Eile |
| sin 5,6° = | 43 km/h | * sin 53° |
| 360 km/h |
Windeinfallwinkel
Windeinfallwinkel = Windwinkel + (Vorzeichen Luv-Winkel)
47,5° = 53° + (- 5,6°)
Windwinkel
Grundgeschwindigkeit = Eile * sin (Windwinkel + (Vorzeichen Luv-Winkel) * csc Windwinkel
330 km/h = 360 km/h * sin (53° + (- 5,6°) * csc 53°
Lee-Winkel (Abdrift in Grad)
| cot Lee-Winkel = | Eile | * csc Windeinfallwinkel - cot Windeinfallwinkel |
| Windgeschwindigkeit in km/h |
| cot 5,46° = | 360 km/h | * csc 47° - cot 47° |
| 43 km/h |
Fahrt über Grund
| Vorhandene Daten | |
|---|---|
| Wegpunkt | BB 17-6 |
| Windrichtung | 255° |
| Windwinkel | 53° Links |
| Luv-Winkel | 6° |
| Windeinfallwinkel | 47° |
| Windgeschwindigkeit |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W |
| Deviation | --- |
| rwK | 308° |
| rwSK | 302° |
| mwSK | --- |
| KSK | --- |
| Temperatur am Boden | 15°C |
| Außentemperatur in Flughöhe | --- |
| Eile | 360 km/h |
| Grundgeschwindigkeit | 330 km/h |
| Fahrt über Grund | --- |
| Flughöhe | 4.500 m |
| Entfernung | 41,79 km |
| Flugdauer | --- |
Ein weiterer wichtiger Punkt für die Navigation fehlt aber noch. Unsere Geschwindigkeit relativ zum Boden (Fahrt über Grund).
Bisher kennen wir nur die Grundgeschwindigkeit (also die Geschwindigkeit durch die Luft unter Einbeziehung von Windeinflüssen) sowie die Kursabweichung durch Windeinflüsse.
Aber auch die uns umgebende Luft selber ändert sich.
Mit zunehmender Höhe sinkt der Luftdruck, und damit auch der Luftwiderstand gegenüber unserer Flugzeugbewegung nach vorne. Unser Fahrtmesser kann aber nur die Druckdifferenz (also den überwundenen Widerstand) gegenüber der umgebenden Luft messen, und uns so die Fahrt (Eile) anzeigen, was uns aber letzten Endes nur die aerodynamisch wichtige Geschwindigkeit anzeigt. Fällt der Luftdruck (und damit der Luftwiderstand) bewegen wir uns in Relation zum Boden deutlich schneller, haben aber im Fahrtmesser die selbe Anzeige wie vorher. Auch die Temperatur der umgebenden Luft beeinflusst dieses und die Temperatur fällt für je 100m zusätzliche Höhe (abhängig von der Luftfeuchtigkeit) um ungefähr 0,65 - 1°C.
Für 'Cliffs of Dover' existiert eine Temperaturtabelle mit den Basiswerten, die wir hier nutzen werden.
| Höhe (km) | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 | 8,5 | 9 | 9,5 | 10 | 10,5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temp. (°C) | 15 | 14 | 10 | 8 | 4 | 1 | -3 | -6 | -9 | -12 | -16 | -19 | -23 | -26 | -30 | -33 | -36 | -39 | -42 | -46 | -49 | -52 |
Eine weitere Möglichkeit sind diverse Umrechnungsseiten im Internet (hier mal eine als Beispiel).
Und zu guter Letzt können wir noch einen befreundeten Bomberpiloten der sich gerade in der passenden Flughöhe befindet bitten, mal auf sein Außenthermometer zu sehen.
Wir gehen also wieder auf die Vorderseite des Dreieckrechners
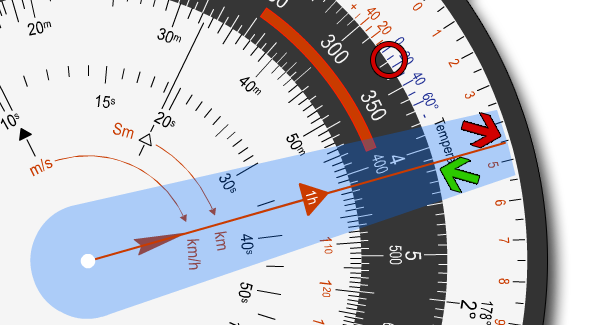
Dort stellen wir auf dem Mittelring die ermittelte Grundgeschwindigkeit von 330 km/h ungefähr auf die aus der Tabelle entnommene Außentemperatur von -12°C auf dem Gradring.
Anschließend stellen wir das Lineal auf die geplante Flughöhe von 4,5 km am äußeren Gradring.
Jetzt können wir am Lineal auf dem Mittelring die Fahrt über Grund von ungefähr 413 km/h ablesen.
Auch diesen Wert tragen wir wieder in die Kursberechnunstabelle ein.
Flugdauer
| Vorhandene Daten | |
|---|---|
| Wegpunkt | BB 17-6 |
| Windrichtung | 255° |
| Windwinkel | 53° Links |
| Luv-Winkel | 6° |
| Windeinfallwinkel | 47° |
| Windgeschwindigkeit |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W |
| Deviation | --- |
| rwK | 308° |
| rwSK | 302° |
| mwSK | --- |
| KSK | --- |
| Temperatur am Boden | 15°C |
| Außentemperatur in Flughöhe | -12°C |
| Eile | 360 km/h |
| Grundgeschwindigkeit | 330 km/h |
| Fahrt über Grund | 413 km/h |
| Flughöhe | 4.500 m |
| Entfernung | 41,79 km |
| Flugdauer | --- |
Jetzt ermitteln wir die Flugdauer
Wir verwenden wieder die Vorderseite des Dreieckrechners.
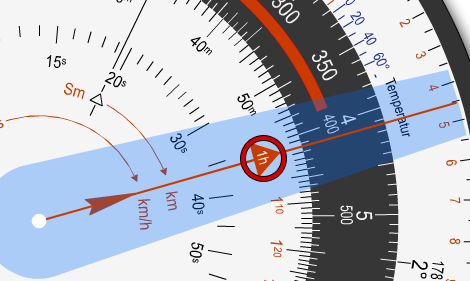
Wir stellen den 1h-Pfeil der Zeitscheibe auf die ermittelte Fahrt über Grund von 413 km/h.
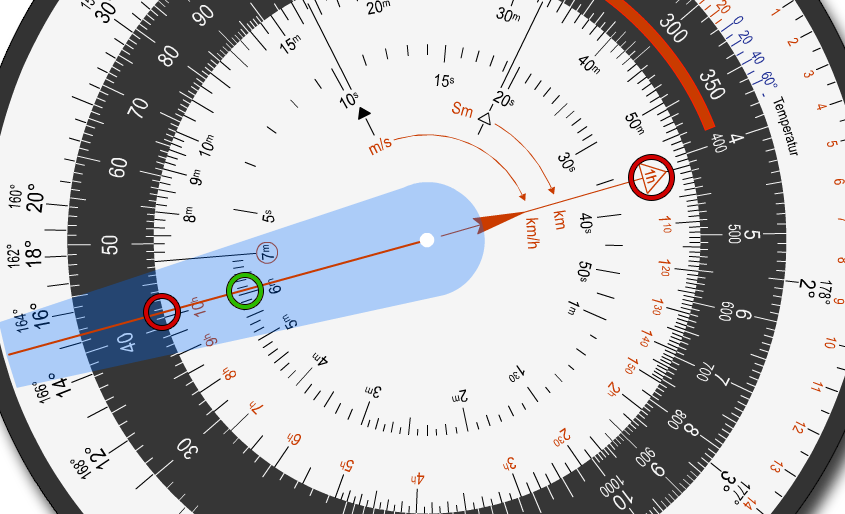
Anschließend verschieben wir das Lineal den m/s-Pfeil auf die Entfernung von 41,8 km im Mittelring und liest auf der Zeitscheibe die Flugdauer ab.
In unserem Beispiel sind das 6 Minuten und 6 Sekunden, die wir ebenfalls in die Kursberechnungstabelle eintragen.
Rechnerischer Weg:
1 km/h = 1 / 3,6 m/s = 0,28 m/s
Entfernung(m)/Fahrt über Grund(m/s) = Flugdauer(s)
Flugdauer(s)/60 = Flugdauer(min)
Also:
413 km/h = 413 / 3,6 m/s = 114,7 m/s
41790 m / 114,7 m/s = 364 s
364 s / 60 = 6:06 min
Kompass- Steuerkurs
| Vorhandene Daten | |
|---|---|
| Wegpunkt | BB 17-6 |
| Windrichtung | 255° |
| Windwinkel | 53° Links |
| Luv-Winkel | 6° |
| Windeinfallwinkel | 47° |
| Windgeschwindigkeit |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W |
| Deviation | --- |
| rwK | 308° |
| rwSK | 302° |
| mwSK | --- |
| KSK | --- |
| Temperatur am Boden | 15°C |
| Außentemperatur in Flughöhe | -12°C |
| Eile | 360 km/h |
| Grundgeschwindigkeit | 330 km/h |
| Fahrt über Grund | 413 km/h |
| Flughöhe | 4.500 m |
| Entfernung | 41,79 km |
| Flugdauer | 6:06 min |
Eine letzte Anpassung bleibt aber noch. Der Kompass Steuerkurs.
In 'Cliffs of Dover' (und auch in der Realität) kommen noch zwei weitere Faktoren ins Spiel, die unseren Kompass im Flugzeug vom geographischen Nordpol ablenken. Die Ortsmissweisung (Deklination) und die Deviation (Ablenkung durch Flugzeuginterne Magnetfelder).
In 'Battle of Stalingrad' können wir diese Anpassung überspringen, da beides nicht simuliert wird. Hier ist der zuvor ermittelste rwSK ebenfalls der KSK..
Korrektur der Ortsmissweisung
Da wir nun unseren rechtweisenden Steuerkurs berechnet haben können wir daraus, mit
Hilfe der Ortsmissweisung, den missweisenden Steuerkurs ermitteln.
Die jeweilige Ortsmissweisung für unseren geplanten Streckenabschnitt können wir der Karte entnehmen. Für 'Cliffs of Dover' beträgt sie 9° West.
Mit der Ortsmissweisung verhält es ähnlich wie mit dem Windwinkel.
West = Ortsmissweisung negativ, Ost = Ortsmissweisung positiv
Für die Berechnung des missweisenden Steuerkurses wird die Ortsmissweisung vom rechtweisenden Steuerkurs abgezogen (rwSK - OM = mwSK).
Also hier:
302° rwSK - (-9° OM) = 311° mwSK
Den rechtweisenden Steuerkurs können wir wieder in die Kursberechnungstabelle eintragen.
Oder als 'Eselsbrücke': Ist die Ortsmissweisung West schlag sie auf den Rest.
Korrektur der Deviation
Da wir nun unseren missweisenden Steuerkurs kennen können wir daraus, mit
Hilfe der zu unserem Flugzeug gehörenden Deviationstabelle, den Kompass-Steuerkurs ermitteln.
| Kurs nach Karte | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deviation | -2 | -1 | 0 | 2 | 3 | 4 | 4 | 3 | 3 | 2 | 1 | 1 | -1 | -3 | -4 | -3 | -1 | 0 | 0 |
| Kurs nach Karte | 180 | 190 | 200 | 210 | 220 | 230 | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 | 360 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deviation | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 0 | -2 | -3 | -3 | -2 | 0 | 1 | 2 | 1 | -1 | -2 | -2 |
Hierzu suchen wir uns in der Deviationstabelle aus der zu unserem (gerundeten) rechtweisenden Steuerkurs passenden Kurs die entsprechende Deviation heraus.
Im aktuellen Beispiel wäre das für den rechtweisenden Steuerkurs von 302° (gerundet 300°) eine Deviation von 0°.
Die so ermittelte Deviation wird vom missweisenden Steuerkurs subtrahiert.
Also hier:
311° mwSK - 0° DEV = 311° KSK
Den Kompass-Steuerkurs und die Deviation tragen wir ebenfalls in die Kursberechnungstabelle ein.
Jetzt haben wir alle nötigen Daten für den ersten Streckenabschnitt zusammengetragen.
Zusammengefasst haben wir jetzt diese Flugparameter:
Kompass- Steuerkurs: 302° (KSK)
Fahrt: 360 km/h (IAS)
Flughöhe: 4.500 m (Barometrisch/Normaldruck)
Entfernung: 41,79 km (Geografisch)
Flugdauer: 6:06 Minuten
Berechnung des zweiten Streckenabschnittes
| Vorhandene Daten | ||
|---|---|---|
| Daten | 1. Streckenabschnitt | 2. Streckenabschnitt |
| Wegpunkt | BB 17-6 | BB 21-5 |
| Windrichtung | 255° | 255° |
| Windwinkel | 53° Links | 102° Links |
| Luv-Winkel | 6° | 7° |
| Windeinfallwinkel | 47° Links | 95° Links |
| Windgeschwindigkeit |
12 m/s
43 km/h |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W | 9° W |
| Deviation | 0° | -2° |
| rwK | 308° | 357° |
| rwSK | 302° | 350° |
| mwSK | 311° | 359° |
| KSK | 311° | 357° |
| Temperatur am Boden | 15°C | 15°C |
| Außentemperatur in Flughöhe | -12°C | -12°C |
| Eile | 360 km/h | 360 km/h |
| Grundgeschwindigkeit | 330 km/h | 365 km/h |
| Fahrt über Grund | 413 km/h | 460 km/h |
| Flughöhe | 4.500 m | 4.500 m |
| Entfernung | 41,79 km | 40,4 km |
| Flugdauer | 6:06 min | 5:17 min |
Die Berechnung des Kurses für den zweiten Streckenabschnitt bitte selbstständig durchführen.
Die ausgefüllte Tabelle dient lediglich der Eigenkontrolle.
Geringfügige Abweichungen sind durch Ungenauigkeiten beim Ablesen des Dreieckrechners unvermeidlich, aber bei größeren Unstimmigkeiten passt irgendwas nicht.
Kurswechselberechnung
| Vorhandene Daten | ||
|---|---|---|
| Daten | 1. Streckenabschnitt | 2. Streckenabschnitt |
| Wegpunkt | BB 17-6 | BB 21-5 |
| Windrichtung | 255° | 255° |
| Windwinkel | 53° Links | 102° Links |
| Luv-Winkel | 6° | 7° |
| Windeinfallwinkel | 47° Links | 95° Links |
| Windgeschwindigkeit |
12 m/s
43 km/h |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W | 9° W |
| Deviation | 0° | -2° |
| rwK | 308° | 357° |
| rwSK | 302° | 350° |
| mwSK | 311° | 359° |
| KSK | 311° | 357° |
| Temperatur am Boden | 15°C | 15°C |
| Außentemperatur in Flughöhe | -12°C | -12°C |
| Eile | 360 km/h | 360 km/h |
| Grundgeschwindigkeit | 330 km/h | 365 km/h |
| Fahrt über Grund | 413 km/h | 460 km/h |
| Flughöhe | 4.500 m | 4.500 m |
| Entfernung | 41,79 km | 40,4 km |
| Flugdauer | 6:06 min | 5:17 min |
| Geänderte Flugdauer | ||
| Durch letzten Kurswechsel | --- | --- |
| Neuer Kurswechsel | --- | --- |
| Durch neuen Kurswechsel | --- | --- |
| Geänderte Entferung | ||
| Während Kurswechsel | --- | --- |
| Anhand geänderter Flugdauer | --- | --- |
Jetzt berechnen wir die Zeit für unsere nötigen Kurswechsel
Wir haben die Daten für beide Streckenabschnitte berechnet.
Natürlich können wir nicht "auf der Stelle" drehen und "um die Ecke" fliegen, deswegen müssen wir den Kurswechselpunkt der vor unserem eigentlichen Wegpunkt liegt berechnen.
Hierzu bedienen wir uns der Faustformel: 1 Minute pro 90°, oder 1,5°/1s, dass entspricht, je nach Geschwindigkeit und Höhe, ungefähr der 30° Standardkurve und ist somit auch ein guter Richtwert für den Flug im Verband. Wird jedoch in Einer Rotte oder alleine geflogen, so ist es vorteilhafter und genauer eine 2-Minuten-Kurve mit Hilfe des Wendezeigers zu fliegen, diese berechnet sich mit 2 Minuten pro 360° oder 3°/1s oder 30 Sekunden pro 90°. Um diese Kurven korrekt zu fliegen braucht es natürlich etwas Übung und Feingefühl. Es bietet sich daher an, die Kurve nach dieser Faustformel bei jeder Gelegenheit zu üben.
Da wir bereits für beide Kurse die Kursberechnung gemacht haben, können wir nun mit Hilfe des Kurswechselwinkels und der Faustformel eine einfache Weg/Zeit-Berechnung für den Kurswechsel mit dem Dreieckrechner durchführen.
Dazu ermitteln wir zunächst den Winkel mit der Rückseite vom Dreieckrechner.
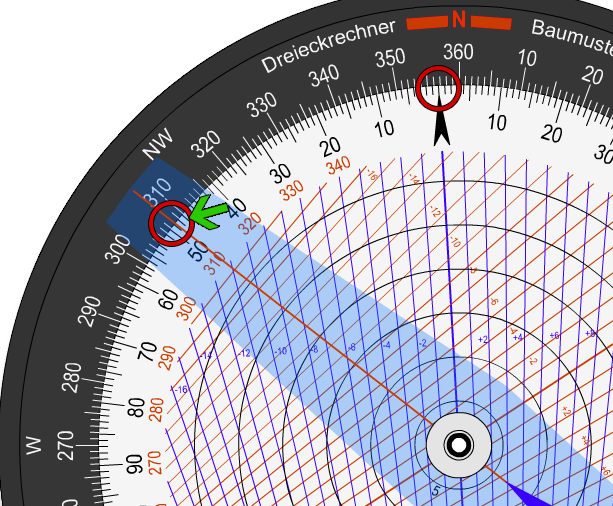
Mit dieser Winkeldifferenz arbeiten wir jetzt auf der Vorderseite weiter. Wir bringen die 90 auf dem Mittelring mit der für einen Kurswechsel von 90 Grad benötigten Zeit auf der Zeitscheibe in Deckung. Das Lineal können wir dabei als Hilfe nutzen. In unserem Fall (die 30-Grad Standartkurve) ist das 1 Minute.
Dafür stellen wir mit der Flugzeugscheibe den rwK nach dem Kurswechsel und mit dem Windlineal den rwK vor dem Kurswechsel ein.
Über das Windlineal erhalten wir dann auf der Flugzeugscheibe die Winkeldifferenz von in diesem Fall 49°.
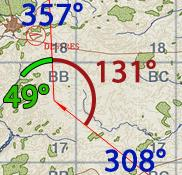
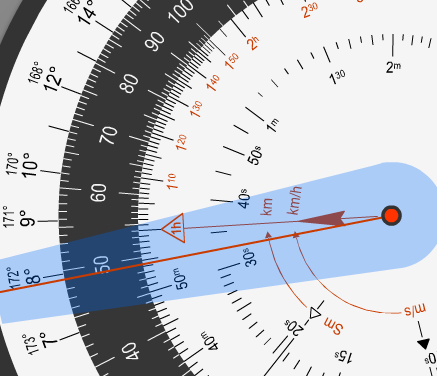
Nun verschieben wir das Lineal auf die Winkeldifferenz auf dem Mittelring und können auf der Zeitscheibe die benötigte Dauer für diese ablesen. In unserem Beispiel sind das 32 Sekunden.
Damit kann man bereits arbeiten.
Wir werden also die Kurve bereits vor erreichen des Wegpunktes einleiten müssen und kommen nach Beendigung der Kurve hinter dem Wegpunkt auf dem neuen Kurs raus.
Also ziehen wir jetzt von den Kursberechnungen beider Streckenabschnitte jeweils die Hälfte der Kurvendauer (also je 16 Sekunden) ab.
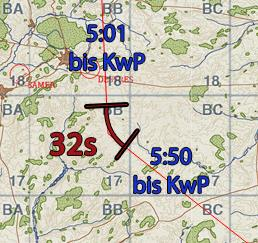
Kurs vor dem KwP: 6:06 min - 16 s
KW
Kurs nach dem KwP: 5:17 min - 16 s
= 5:50 min
= 0:32 min
= 5:01 min
Die Kurswechseldauer und die geänderten Flugzeiten für beide Streckenabschnitte notieren wir uns ebenfalls. Hinweis: ob wir nach 'rechts' oder 'links' die Kurve fliegen müssen können wir uns als Arbeitserleichterung ebenfalls notieren.
Wobei wir uns die geänderte Flugdauer für den aktuellen Streckenabschnitt sowie die Kurswechseldauer auch für diesen notieren (und eine ggf. bereits vorhandene Änderung durch einen vorhergehenden mit einbeziehen). Die geänderte Flugdauer für den folgenden Streckenabschnitt notieren wir uns im folgenden Streckenabschnitt.
Zur Veranschaulichung zeichne ich den Kurswechselpunkt und die Kurve noch in die Karte ein.
In den 'Vorhandenen Daten' würde also für unseren Kurswechsel nach dem ersten Streckenabschnitt folgendes stehen:
| Vorhandene Daten | ||
|---|---|---|
| Daten | 1. Streckenabschnitt | 2. Streckenabschnitt |
| Wegpunkt | BB 17-6 | BB 21-5 |
| Fahrt über Grund | 413 km/h | 460 km/h |
| Entfernung | 41,79 km | 40,4 km |
| Flugdauer | 6:06 min | 5:17 min |
| Geänderte Flugdauer | ||
| Durch letzten Kurswechsel | --- | 5:01 min |
| Neuer Kurswechsel | 0:32 min | --- |
| Durch neuen Kurswechsel | 5:50 min | --- |
| Geänderte Entferung | ||
| Während Kurswechsel | --- | --- |
| Anhand geänderter Flugdauer | --- | --- |
Mit dem aktuellen Streckenabschnitt sind wir jetzt soweit fertig, das wir auch eine finale Flugdauer dafür haben. Alle anderen Daten sind ebenfalls ermittelt worden.
Sofern wir im aktuellen Streckenabschnitt einen Kurswechsel und/oder eine geänderte Flugdauer haben sollte jetzt ja auch in unseren Aufzeichnungen irgendwo mindestens eine Eintragung stehen.
Die jeweils zurückgelegten Entfernungen können wir (anhand der Zeitangaben und der Fahrt über Grund) ebenfalls ermitteln.
Dabei hilft uns erneut der Dreieckrechner.
Auf der Vorderseite bringen wir den 1-Stunden-Pfeil mit der entsprechenden Fahrt über Grund auf dem Mittelring in Deckung.
Das Lineal verschieben wir auf die jeweilige Flugdauer.
Am Mittelring können wir dann die in dieser Zeit zurückgelegte Entfernung ablesen.
Für einen Kurswechsel (sofern vorhanden) benutzen wir die Dauer der Kurve und die mittlere Fahrt über Grund aus beiden angrenzenden Streckenabschnitten.
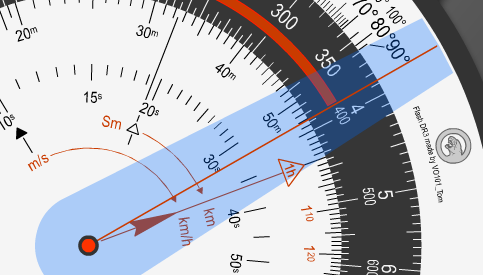
In unserem Beispiel also
Fahrt über Grund: 437 km/h
(413 km/h + 460 km/h) / 2 = gerundet 437 km/h
Dauer: 0:32 min
Abgelesene Entfernung: 3,9 km
Für durch Kurswechsel geänderte Flugdauern (sofern vorhanden) benutzen wir die zuletzt gemachte Eintragung für die Flugdauer sowie die Fahrt über Grund aus dem aktuellen Streckenabschnitt.
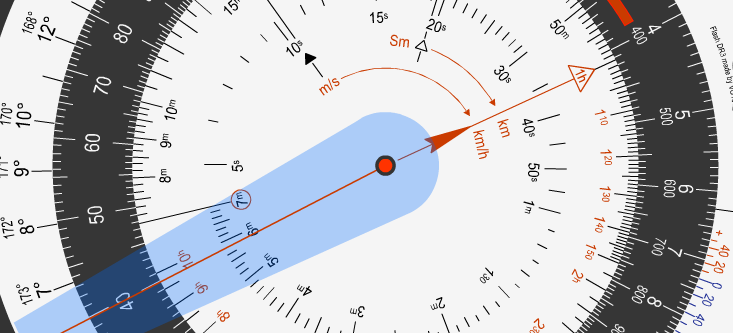
In unserem Beispiel also
Fahrt über Grund: 413 km/h
Dauer: 5:50 min
Abgelesene Entfernung: 40 km
Dieses notieren wir uns wieder.
In den 'Vorhandenen Daten' sind jetzt also für den ersten Streckenabschnitt alle Daten eingetragen:
| Vorhandene Daten | ||
|---|---|---|
| Daten | 1. Streckenabschnitt | 2. Streckenabschnitt |
| Wegpunkt | BB 17-6 | BB 21-5 |
| Fahrt über Grund | 413 km/h | 460 km/h |
| Entfernung | 41,79 km | 40,4 km |
| Flugdauer | 6:06 min | 5:17 min |
| Geänderte Flugdauer | ||
| Durch letzten Kurswechsel | --- | 5:01 min |
| Neuer Kurswechsel | 0:32 min | --- |
| Durch neuen Kurswechsel | 5:50 min | --- |
| Geänderte Entferung | ||
| Während Kurswechsel | 3,9 km | --- |
| Anhand geänderter Flugdauer | 40 km | --- |
Die Berechnung der Entfernung für den zweiten Streckenabschnitt bitte mal selber durchführen.
Es sollten ungefähr 38 km dabei herauskommen.
Zusammenfassung der Flugdaten
| Vorhandene Daten | ||
|---|---|---|
| Daten | 1. Streckenabschnitt | 2. Streckenabschnitt |
| Wegpunkt | BB 17-6 | BB 21-5 |
| Windrichtung | 255° | 255° |
| Windwinkel | 53° Links | 102° Links |
| Luv-Winkel | 6° | 7° |
| Windeinfallwinkel | 47° Links | 95° Links |
| Windgeschwindigkeit |
12 m/s
43 km/h |
12 m/s
43 km/h |
| Ortsmissweisung | 9° W | 9° W |
| Deviation | 0° | -2° |
| rwK | 308° | 357° |
| rwSK | 302° | 350° |
| mwSK | 311° | 359° |
| KSK | 311° | 357° |
| Temperatur am Boden | 15°C | 15°C |
| Außentemperatur in Flughöhe | -12°C | -12°C |
| Eile | 360 km/h | 360 km/h |
| Grundgeschwindigkeit | 330 km/h | 365 km/h |
| Fahrt über Grund | 413 km/h | 460 km/h |
| Flughöhe | 4.500 m | 4.500 m |
| Entfernung | 41,79 km | 40,4 km |
| Flugdauer | 6:06 min | 5:17 min |
| Geänderte Flugdauer | ||
| Durch letzten Kurswechsel | --- | 5:01 min |
| Neuer Kurswechsel | 0:32 min Rolf | --- |
| Durch neuen Kurswechsel | 5:50 min | --- |
| Geänderte Entferung | ||
| Während Kurswechsel | 3,9 km | --- |
| Anhand geänderter Flugdauer | 40 km | 38 km |
Aus der Masse an gesammelten Daten erstellen wir uns jetzt einen Flugplan.
Im Flugzeug selber interessieren uns allerdings nur die wirklich nötigen Daten. Der Wegpunkt, der am Kompass abzulesende Kurs, die Eile, die zu fliegende Höhe, die Entfernung zum nächsten Wegpunkt (rein zur Orientierung) und die Flugdauer.
Alles weitere ist nur wichtig, wenn wir unsere Berechnung nochmal überprüfen wollen oder schlimmstenfalls dabei einen Fehler gemacht haben.
Also wie tragen wir die Daten jetzt sinnvoll ein?
In die erste Zeile kommt der Anfangspunkt (unser erster Wegpunkt). Sonst nichts.
In die nächste Zeile kommen die Flugparameter ab diesem Punkt bis zum nächsten Wegpunkt. Also (am Kompass abzulesender) Kurs, Eile, Höhe, Entfernung zum nächsten Wegpunkt und die Flugdauer.
In die folgende Zeile kommt der nächste Wegpunkt.
Hier können wir uns zusätzliche Informationen reinschreiben.
Im konkreten Fall wollen wir unseren Kurs ändern und dabei für 32 Sekunden eine Kurve nach rechts Fliegen. Auch die Entfernung haben wir berechnet.
Ausser dem Wegpunkt selber können wir also bei KSK ein 'Rolf' bei Entfernung '3,9 km' und bei Flugdauer '0:32 min' eintragen. Wir können also sehr einfach sehen in welche Richtung und wie lange wir drehen müssen und haben zur groben Orientierung noch die Entfernung parat. Der neue Kurs steht dann wieder in der nächsten Zeile.
Hier stehen dann wieder die Flugparameter bis zum nächsten Wegpunkt. Kurs, Eile, Höhe, Entfernung zum nächsten Wegpunkt und die Flugdauer.
Je nach Anzahl der Wegpunkte wird sich dieses wiederholen.
In der letzten Zeile steht dann der Endpunkt des geplanten Kurses. Als weitere Details kann man Dinge wie 'Platzrunde', 'Ziele angreifen'... angeben.
Die meisten Flugparameter (KSK, Eile, Höhe) sind ja eindeutig.
Bei der Entfernung und Flugdauer nehmen wir die jeweils letzte Eintragung aus den vorhandenen Daten. Falls wir durch einen Kurswechsel Zeiten und Entfernungen neu berechnet haben suchen wir uns die jeweils letzte Eintragung raus. Ansonsten übernehmen wir die unveränderten Werte aus den entsprechenden Daten.
Zur Veanschaulichung hab ich hier mal die Flugplantabelle und die (auf die wichtigen Werte) reduzierten vorhandenen Daten nebeneinandergesetzt und entsprechend farblich markiert.
| Flugplan: | |||||
|---|---|---|---|---|---|
| Wegpunkt | KSK | Eile | Höhe | Entfernung | Flugdauer |
| BE 15-3 | |||||
| 311° | 360 km/h | 4.500 m | 40 km | 5:50 min | |
| BB 17-6 | Rolf | 3,9 km | 0:32 min | ||
| 359° | 360 km/h | 4.500 m | 38 km | 5:01 min | |
| BB 21-5 | |||||
| Besonderes: | |||||
|
Daten des Flugplanes
innerhalb der Blockschulung |
|||||
| Gesamtflug: | |||||
| Wegpunkte | Entfernung | Flugdauer | |||
| 3 | 81,9 km | 11:23 min | |||
| Vorhandene Daten | ||
|---|---|---|
| Daten | 1. Streckenabschnitt | 2. Streckenabschnitt |
| Wegpunkt | BB 17-6 | BB 21-5 |
| KSK | 311° | 357° |
| Eile | 360 km/h | 360 km/h |
| Flughöhe | 4.500 m | 4.500 m |
| Entfernung | 41,79 km | 40,4 km |
| Flugdauer | 6:06 min | 5:17 min |
| Geänderte Flugdauer | ||
| Durch letzten Kurswechsel | --- | 5:01 min |
| Neuer Kurswechsel | 0:32 min Rolf | --- |
| Durch neuen Kurswechsel | 5:50 min | --- |
| Geänderte Entferung | ||
| Während Kurswechsel | 3,9 km | --- |
| Anhand geänderter Flugdauer | 40 km | 38 km |
Hier mal als Beispiel ein komplett ausgefüllter Flugplan
| Flugplatz | Muster | Kraftstoff | Zuladung |
|---|---|---|---|
|
Marquise West
(BA 20-1) |
Bf 109 E4
Schwarze 5 W-Nr.: 8274 |
300 kg
400 l |
- |
| Wetterinformation | |||
|
Bewölkt ab 1500/beständig
Wind: 0 m/s aus 0° Temperatur: 15°C NN |
| Flugplan: | |||||
|---|---|---|---|---|---|
| Wegpunkt | KSK | Eile | Höhe | Entfernung | Flugdauer |
| AZ 18-5 | Zirkus | ||||
| 277° | 420 km/h | 1.500 m | 95 km | 11:45 min | |
| AQ 18-7 | Rolf | 6,5 km | 0:50 min | ||
| 354° | 420 km/h | 1.500 m | 36 km | 3:55 min | |
| AP 22-5 | Rolf | 5 km | 0:38 min | ||
| 56° | 420 km/h | 1.500 m | 36 km | 4:15 min | |
| AR 24-9 | Rolf | 3,1 km | 0:24 min | ||
| 91° | 420 km/h | 1.500 m | 64 km | 7:31 min | |
| AY 25-7 | Rolf | 7,6 km | 0:56 min | ||
| 172° | 420 km/h | 1.500 m | 57 km | 6:53 min | |
| AZ 20-5 | Zirkus | ||||
| Heimatkurs: | 145° | ~2:20 min | |||
| Einflug: BA 19-6 | Platzrunde | ||||
| Besonderes: | |||||
|
-Startzeit zwischen 2000 und 2030
-Sonderlichtzeichen im Raum Boulogne (AZ 19-2) mit Zeichen: AR/+ -Sonderlichtzeichen im Raum Gap Griz Nez (AZ 20-5) mit Zeichen: OS/: -Sonderfunkzeichen im Raum Audembert (BA 20-5) auf Frequenz: 299:00 MHz (beleuchtet, Zeichen: 1) -Sonderfunkzeichen im Raum Dünkirchen-West/Grand-Fort-Philippe (BD 22-5) auf Frequenz: 300:00 MHz -Landeplatz ist für Nachtlandung ausgerüstet, es ist keine Verdunklung zu erwarten -Wegpunkte, Flugzeit und Entfernung sind von Zirkus bis Zirkus Zusätzliche Flugzeit zum Anflug auf ersten Wegpunkt, Zirkus am ersten und letzten Wegpunkt der Route sowie für Erreichen des Landeplatzes inclusive Platzrunde und Landung bei der Kraftstoffplanung berücksichtigen. |
|||||
| Gesamtflug: | |||||
| Wegpunkte | Entfernung | Flugdauer | |||
| 6 | 310,2 km | 37:07 min | |||